Planimetria dowód Diokona: Mamy dowolny trójkąt ostrokątny ABC, w którym wysokości przecinają się w punkcie H. Udowodnij, że promienie okręgów opisane na trójkątach ABC, ABH, BCH, ACH są sobie równe. Kombinuję z twierdzeniem sinusów i kątami przyległymi, ale jakoś mi nie idzie. Ma ktoś może jakiś pomysł?

iks: http://www.matematyka.wroc.pl/ligazadaniowa/kwiecien-2015-2

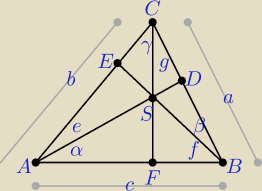
Bogdan: D, E, F − spodki wysokości trójkąta ABC, S − ortocentrum, R − długość promienia okręgu opisanego na ΔABC R_A − długość promienia okręgu opisanego na ΔBCS Teza: R = R_A Dowód: ΔFBC: g = 90^o − β − f ΔABE: α + e = 90^o − f = 90 − f + β − β = β + g ⇒ sin(α+e) = sin(β+g) = sin[180^o−(β+g)] Z twierdzenia sinusów: ΔABC: a = 2R*sin(α + e) i ΔBCS: a = 2R_A*sin[180^o − (β + g)] ⇒ R = R_A analogicznie w pozostałych przypadkach.

Diokona: Dziękuję kolego . Teraz będzie z górki.

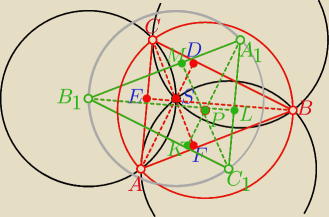
Bogdan: Dorzucając jeszcze 3 grosze w tym wątku dodam, że można tu odkryć ciekawe zależności między elementami trójkątów i okręgów, np.: S − ortocentrum trójkąta ABC i środek okręgu opisanego na trójkącie A₁B₁C₁. P − ortocentrum trójkąta A₁B₁C₁ i środek okręgu opisanego na trójkącie ABC.