zadanie z parametrem jaros: Wyznacz wszystkie wartości parametru c, dla których równanie x³+6cx²−15c²x+24c=0 ma trzy rozwiązania. Nie chodzi mi tutaj o rozwiązanie tego zadania, ponieważ wiem jak je zrobić w przypadku gdy potrzebuje 3 rozwiązań, lecz jakie warunki będą w przypadku 2, 1 oraz 0 rozwiązań?

wredulus_pospolitus: 0 rozwiązań −−−− brak takiej możliwości 2 rozwiązania −−− jedno rozwiązanie jest 'podwójne' 1 rozwiązanie −−− wielomian jest postaci (x − x₁)*(x² + nx + m) i delta w tym drugim nawiasie mniejsza od zera

Jerzy: @Bleee ... w ostatnim przypadku dodatkowo Δ = 0 i pierwiastek równy x₁

jaros: Jeżeli w tym przypadku 2 rozwiązania w czym jedno podwójne to jak mamy postąpić z ekstremami pochodnej?

wredulus_pospolitus: Jerzy −−− racja

wredulus_pospolitus: jaros −−− wyjaśnij o co się pytasz

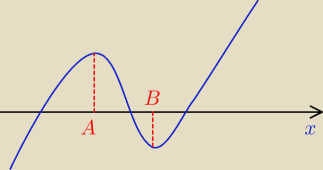
jaros: Powiem to jak to jest w zdaniu wyżej, rozwiązania z tego co wiem zawsze zależą od ekstremum, (przyjmijmy, że funkcja ma kreska w punktach A oraz B) więc dla 3 rozwiązań iloczyn funkcji podanej w poleceniu (nazwijmy g(x) oraz liczmy g(A)*g(B)) jest <0 by otrzymać 3 rozwiązania, I Tutaj jest moje pytanie jak wygladała by ta funkcja zależna od parametru by otrzymać 2 rozwiązania?

wredulus_pospolitus: jaros −−− rozpatrując wielomiany stopnia trzeciego: przy 2 rozwiązaniach −−− jedno z rozwiązań będzie jednocześnie ekstremum funkcji ... więc g'(A) * g'(B) = 0 przy 1 rozwiązaniu −−− jeżeli mamy jedną z opcji: a) brak ekstrem funkcji (jest tylko punkt przegięcia) b) g'(A) * g'(B) > 0

wredulus_pospolitus: bez znaku pochodnej powinienem pisać

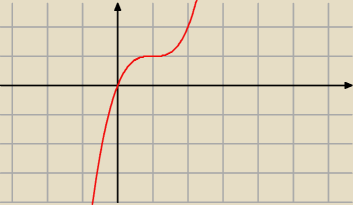
PW: Zastanów się o co chcesz spytać i sformułuj to poprawnie. Mówisz "rozwiazania zawsze zależą od ekstremum". Rzeczywiście?