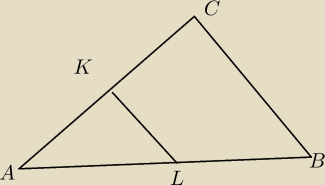
geometria analityczna salamandra: Na bokach AC i AB trójkąta ABC o wierzchołkach A = (−1, −1), B = (11, 4) i C = (5, 8),

	5
wybrano punkty K i L odpowiednio, w ten sposób, ze˙ KL k CB. Pole trapezu BCKL stanowi
	9

pola trójkąta ABC. Zatem A) K = (1, 2) B) K = (7, 2) C) K = (3, 5) D) K = (4, 6)

	1		1
PABC=		|(11+1)(8−1)−(4−1)(5+1)|=		|12*7−3*6|=33
	2		2

	5		55
PBCKL=		*33=
	9		3

	44
PAKL=
	3

Wiem, że mógłbym podstawić każdy punkt po kolei, wyznaczyć równanie prostej równoległej do CB, do niej prostopadłej czyli wysokość trapezu, ale jaki jest uniwersalny sposób, żeby nie strzelać?

wredulus_pospolitus:

	5		4
skoro trapez stanowi		pola całego trójkąta to mały trójkąt stanowi
	9		9

	4		2
więc boki małego trójkąta stanowią (		)1/2 =		boków dużego trójkąta
	9		3

więc punkt K leży w proporcji 2:3 na boku AC stąd:

5 − (−1)
	*2 + (−1) = 3
3

8 − (−1)
	*2 + (−1) = 5
3

czyli K = (3,5) odpowiedź (C)

wredulus_pospolitus: oczywiście ... K leży w proporcji 2 : 1 na boku AC

wredulus_pospolitus: PS. Bez liczenia ... a patrząc na odpowiedzi (B) −−− odpada (współrzędna 'x' jest większa od tej dla punktu C) (D) −−− odpada (nie leży na odcinku AC)

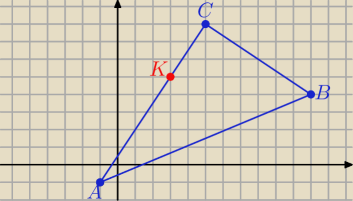Mila: ΔAKL∼ΔABC

	44/3		4
k2=		=
	33		9

	2
k=
	3

	2
AK→=		AC→ wsp. AC odczytuję z rysunku, bo można przy tych danych
	3

	2
AK→=[x+1,y+1]=		*[6,9]
	3

x+1=4 i y+1=6 x=3 i y=5 K=(3,5)