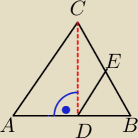
planimereia jaros: W trójkącie równoramiennym podstawa ma długość "a", a wysokość opuszczona na tę podstawę jest równa odcinkowi, który łączy środek ramienia ze środkiem podstawy. Wyznacz obwód tego trójkąta. Problem w tym, że nie rozumiem dlaczego trójkąt DBE jest równoboczny

fil: a po co ci to? Wyznacz h w zaleznosci od 'a', nastepnie |CB| i liczysz obwod

fil: jednak nie

jaros: no ale jak wyznacze h w zaleznosci od a jak mam 1 rówanie z pitagorasa

fil: Zobacz z trojkatami podobnymi.

Bogdan:

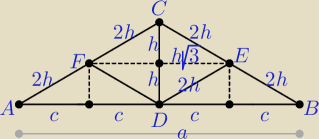
	1
c =		a i c = √ 4h2 + h2 = h√3, zatem |BE| = |EC| = |CF| = |FA| = 2h
	4

1
	a = h√3 ⇒ h = ...
4

jaros: Z czego to wynika, że mamy odcinki uzależnione od h na ramionach trójkąta?

jaros: bb

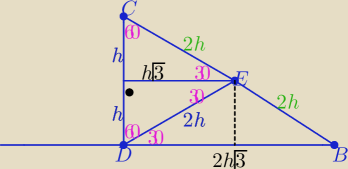
Eta: Z trójkąta "ekierki" (30^o,60^o,90^o) jasne ?

jaros: Hmmm no ale skąd mamy informacje, że kąty powstające przy podstawie mają właśnie 60 raz 30?

Eta: W Δ DES (S −− środek wysokości CD

	h		1
sinα=		=		⇒ α=30o
	2h		2

jaros: No ale znowu skąd mamy informacje, że na połowa ramienia to 2h?

Eta: Z treści zadania!

jaros: Aaaaaa no dobra, już rozumiem dziękuje ślicznie

Magda: Mógłby mi ktoś wskazać, która część w poleceniu właśnie mówi o tym, żę połowa ramienia jest równa 2h

Magda: ?

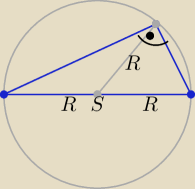
Eta: Środkowa poprowadzona z wierzchołka kąta prostego ma długość równą połowie długości przeciwprostokątnej !