Rozpatrujemy wszystkie czworokąty ABCD , które są jednoczenie wpisane w okrąg i opisane na
okręgu, w których |AB | = 2x , |BC | = 5x , i których obwód jest równy 10.
Pole czworokąta ABCD wpisanego w okrąg można obliczyć ze wzoru Brahmagupty
P = √(p − a)(p − b)(p − c)(p − d )
gdzie p – jest połową obwodu czworokąta.
Zapisz pole czworokąta ABCD jako funkcję zmiennej x . Wyznacz dziedzinę tej funkcji i oblicz
długości boków tego z rozważanych czworokątów, którego pole jest największe.
Niech AB=2x, BC=5x, DC=t, AD=y
Z warunku wpisywalności okregu w czworokąt:
2x+t=y+5x
Obwód: 7x+t+y=10
7x+t=10−y
7x+t−5=5−y
Z warunku wpisywalności:
−3x+t=y
Wstawiam do obwodu:
7x+t−5=5+3x−t
4x+2t=10
2t=10−4x
t=5−2x
wyliczam y:
−3x+t=y
−3x+5−2x=y
y=−5x+5
P=√(5−2x)(5−5x)(5+5x−5)(5−5+2x)=√100x4−350x3+250x2
f(x)=100x4−350x3+250x2
f'(x)=400x3−1050x2+500x
f'(x)=0 ⇔ 400x3−1050x2+500x=0
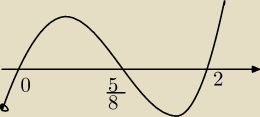
| 5 | ||
x=0 v x= | v x=2 | |
| 8 |
| 5 | ||
max dla x= | ||
| 8 |
| 5 | 25 | 5 | 15 | 15 | ||||||
Więc boki: AB= | , BC= | , CD=5− | = | , AD= | ||||||
| 4 | 8 | 4 | 4 | 8 |
x > 0 i t > 0 i y >0 ⇒D:x∊(0, 1)
a wynik ok? Wiem, że robiłeś 