stereometria mr t: Na kuli o promieniu 𝑅 opisano ostrosłup prawidłowy czworokątny o najmniejszej objętości. Wyznacz długość jego wysokości.

	2R√2H2+a2+a
wyliczyłem a=		, czyli pole podstawy już mam, nastepnie podstawiając do
	H

wzory na objetość ostroslupa i tak mam 2 niewiadome... Da się to jakoś inaczej zrobić?

mr t: rysunek wyszedł beznadziejnie, mam nadzieje ze cokolwiek widac

Bogdan:

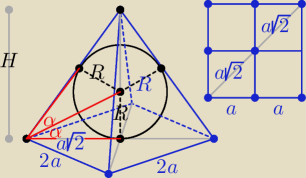
	R
Proponuję w ten sposób: tgα =
	a√2

H		2tgα		2R     a√2
	= tg(2α} =		=
a√2		1 − tg2α		R2   1 −   2a2

	4a2R
H =
	2a2 − R2

	1		4a2R		4		a4R
Objętość V =		*4a2*		=		*
	3		2a2 − R2		3		2a2 − R2

	a4R
Wyznaczamy minimum funkcji f(a) =
	2a2 − R2

Bogdan:

	16
Poprawiam chochlika V =		*f(a)
	3