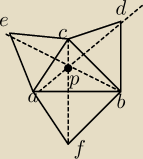
Trójkąt Elena: Niech P będzie punktem Brokara trójkąta ABC, R promieniem okręgu opisanego na ABC, R₁,R₂,R₃ promieniami okręgów opisanych na ABP,BCP,CAP. Udowodnić, że R₁ * R₂ * R₃ = R³ Mam problem w zrozumieniu rozwiązania przedstawionego w książce:

	AB
Początek jest ok, czyli korzystamy z tw sinusów i : R1 =		,
	2sin(∡APB)

	BC		CA
R2=		i R3 =		jednak dalej nie rozumiem skąd równość:
	2sin(∡BPC)		2sin(∡CPA)

sin∡APB = sin∡A , sin∡BPC = sin∡B i sin∡CPA = sin∡C ?