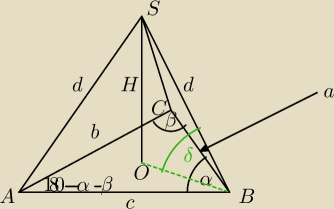
stereometria salamandra: Podstawą ostrosłupa jest trójkąt o danych kątach α i β . Wszystkie krawędzie boczne mają długość d i są nachylone do płaszczyzny podstawy pod kątem o mierze δ . Oblicz objętość tego ostrosłupa. 1. Z tw. sinusów w OBS

H		d
	=
sinδ		sin90

H=d*sinδ 2. Skoro wszystkie krawędzie są nachylone pod takim samym kątem, to spodek wysokości znajduje się w środku okręgu opisanego na podstawie OB=R Z tw. Pitagorasa w OBS H²+R²=d² d²*sin²δ+R²=d² R²=d²−d²*sin²δ R²=d²(1−sin²δ) R²=d²*cos²δ R=d*cosδ <−−−− tu mam wątpliwość czy mogłem tak zrobić

b
	=2R
sinα

b=2d*cosδ*sinα c=2d*cosδ*sinβ a=2d*cosδ*sin(α+β)

	2d3*cos3δ*sinα*sinβ*sin(α+β)
Pp=		=d2*cos2δ*sinα*sinβ*sin(α+β)
	2d*cosδ

	d3*cos2δ*sinδ*sinα*sinβ*sin(α+β)
V=
	3

Jest ok?

jokeros2000: Raczej wszystko dobrze. Co do promienia nie wydaje mi się żeby cosinus był ujemny

jokeros2000: Pole podstawy zamiast 2 powinieneś wpisać raczej 8 chyba że coś przeoczyłem

Mila: 1) punkt, komentarz o spodku wysokości ostrosłupa. W ΔSOB:

	H
sinδ=		⇔H=d*sinδ
	d

	R
cosδ=		⇔R=d*cosδ
	d

2) Obliczenie długości boków ΔABC , pola Δ, V.

salamandra: No zrobiłem, pytanie czy dobrze? @jokeros, tak, na pewno tam powinno być 8