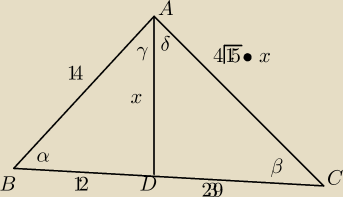
planimetria salamandra: Punkt D leży na boku BC trójkąta ABC oraz |AB | = 14 , |BD | = 12 , |CD | = 239 i |AC | = 4p{15| . Oblicz pole trójkąta ABC. z tw. cosinusów w ABD x²=196+144−336cosα x²=340−336cosα w ΔABC 240x²=196+63001−7028cosα 240x²=63197−7028cosα Wstawiam z pierwszego do drugiego: 240*(340−336cosα)=63197−7028*cosα 81600−80640cosα=63197−7028cosα 18403=73612cosα

	1
cosα=
	4

	√15
więc sinα=
	4

	1		√15		1757√15
PABC=		*14*251*		=
	2		4		4

Jest ok?

annabb: a w treści coś napisali o tym x?

ICSP: |AB| = 14 |AC| = 4√15 |BC| = 251 i wzór Herona leci.

salamandra: sory, ucięło treść: AC=4√15*AD i przyjąłem, że AD=x

salamandra: ICSP, gdyby AC=4√15 to nie można by w ogóle zbudować trójkąta, od tego zacząłem analizę i Heron by wleciał, ale nie zauważyłem, że jest 4√15*AD

ICSP: a jednak nic nie leci 14 + 4√15 < 12 + 239 i koniec zadania.

ICSP: Sposób jak najbardziej dobry.