Trójkąt Elena: Niech A₁, B₁ , C₁ będą rzutami punktu P na boki BC, AC i AB trójkąta ABC, a R promieniem

	BC*AP
okręgu opisanego. Udowodnij, że B1C1 =
	2R

Ktoś ma pomysł w jaki sposób można tego dowieść?

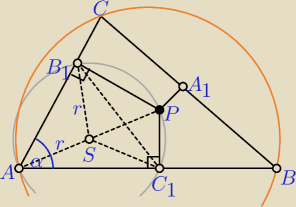Bogdan: Na czworokącie AB₁PC₁ można opisać okrąg o promieniu r, ten sam okrąg jest opisany na trójkącie AB₁C₁.

	|B1C1|
Z twierdzenia sinusów w trójkącie AB1C1:		= 2r = |AP|
	sinα

	|BC|
Z twierdzenia sinusów w trójkącie ABC:		= 2R
	sinα

	|B1C1|		|BC|
Stąd sinα =		i sinα =		⇒ |B1C1| = ....
	|AP|		2R