granica TłumokMatematyczny: Dla jakiej wartości parametru m funkcja

	⎧	x2+4x−5+m dla x≤0
f(x) =	⎩	2x−1 dla x>0	ma granicę w punkcie x=0? Naszkicuj wykres tej

funkcji dla wskazanej wartości m. Mam rozwiązanie tego zadania ale go nie rozumiem. Najpierw obliczono miejsca zerowe tych funkcji i wyszło, że ta pierwsza funkcja: g(0)=−5+m i druga funkcja: h(0)=−1 Nastepnie zrobiono coś takiego (co tez nie wiem skad sie wzielo) −1=−5+m m=4 I narysowano wykres. Proszę o wytłumaczenie kroków w tym zadaniu bo chciałabym umieć rozwiązywać te typy zadań.

ABC: jakieś zwulgaryzowane to twoje rozwiązanie − badamy istnienie granicy lewostronnej w punkcie −badamy istnienie granicy prawostronnej w punkcie jeżeli obie istnieją i są sobie równe to funkcja ma granicę w punkcie

TłumokMatematyczny: Pierwszy raz słyszę o czymś takim jak granica lewostronna i prawostronna....

TłumokMatematyczny: Czemu obliczono te miejsca zerowe i czemu potem te funkcje przyrównano?

HGH: Jeśli pierwszy raz słyszysz o czymś takim jak granica lewo i prawo stronna to zacznij od łatwiejszych przykładów. Kiedy granica istnieje w punkcie?

a7: to nie miejsca zerowe to wartości funkcji dla x=0

a7: http://matematykadlastudenta.pl/strona/931.html aby istaniała granica w x=0 funkcja musi być ciągła a wartości równe sobie

a7: http://matematykadlastudenta.pl/strona/933.html

HGH: Jeśli funkcja f(x) jest ciągła w punkcie x0, to ma w tym punkcie granicę równą f(x0) szukamy granicy w x=0 prawostronna granica w tym punkcie będzie równa −1, liczysz to z funkcji h(x) aby ta granica istniała, g(x) w tym punkcie musi być równe granicy prawostronnej w 0 (czyli −1) przyrównujesz g(x)= −1 i stąd masz m=4.

ABC: nie mieszajcie Tłumokowi w głowie, funkcja nie musi być ciągła w punkcie żeby mieć w nim granicę, nawet nie musi być w tym punkcie określona

Jerzy: Jedno co pewne, to lewostrnna równa prawostronnej.

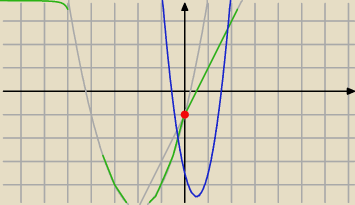
a7: gdyby m nie było równe 4 parabola w zerze mogłaby być np niebieska, nie byłoby ciągłości funkcji nie mogłoby być granicy w zerze

ABC: a7 a funkcja sin x/x nie jest określona w zerze a ma granicę równą jeden

a7: hmm, to może ja coś źle pamiętam sorry w takim razie

ABC: pewnie miałaś na myśli ciągłość funkcji, wtedy musi istnieć granica w punkcie, wartość w punkcie i muszą być równe sobie

a7: no mówię o ciągłości fukcji w punkcie x=0

ABC: ale Tłumok ma zbadać istnienie granicy a nie ciągłość

a7: coś mi się wydawało, że jedno jest warunkiem drugiego, ale to było chyba na odwrót w każdym bądź razie wartości funkcji muszą być równe