zadanie z parametrem
jaros: | | 1 | |
Wyznacz wartości parametru a, dla których równanie x4 + |
| = a ma rozwiązanie. |
| | x4 | |
Widzę tutaj twierdzenie o tym, że suma liczby dodatniej i jej odwrotności, jest zawsze większa
równa 2, ale czy da się tutaj z niego skorzystać?
10 maj 19:34
10 maj 19:37
a7:
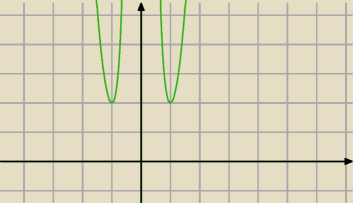
10 maj 19:38
fil: Zly wykres
10 maj 19:38
wredulus_pospolitus:
tak ... masz z niego skorzystać
dla a ≥ 2 powyższe równanie będzie miało rozwiązania
10 maj 19:39
ABC:
niech x+1/x =a to x2+1/x2=a2−2 i jeszcze raz do kawdratu
x4+1/x4=(a2−2)2−2=a4−4a2+2
teraz z uwagi na parzyste potęgi wystarczy znaleźć zbiór wartości tego wyrażenia gdy a∊<2,+∞)
10 maj 19:41
10 maj 19:43
10 maj 20:15
ABC:
na maturze rozszerzonej jeszcze jakaś uwaga by się przydała przy tym sposobie dlaczego "nie ma
dziur"
granica w plus nieskończoności to plus nieskończoność i funkcja ciągła
10 maj 20:23
Saizou :
Do rozwiązania
Milusińskiej komentarz dlaczego "rozciąga się" to na całą dziedzinę

10 maj 20:27
jaros: No chyba badamy zależności pomiędzy średnią arytmetyczną a geometryczną tak? w rozwiązaniu
@Milusińskiej?
10 maj 20:54
jaros: @ABC w twoim sposobie skąd się wzięło w 2 równaniu −2?
10 maj 20:54
Saizou :
Tak, ale ta nierówność spełniona jest dla każdego x≥0, dlatego niezbędny jest komentarz
o parzystości funkcji.
10 maj 20:55
jaros: a nie tylko x>0? Przecież 0 występuje w mianowniku
10 maj 20:58
Saizou :
| | a+b | |
słusznie, ale ogólnie nierówność |
| ≥ √ab jest prawdziwa dla a,b ≥ 0 |
| | 2 | |
10 maj 21:00
ABC: | | 1 | |
jaros bo x* |
| =1  |
| | x | |
10 maj 21:01
jaros: @Saizou a nie wystarczył by komentarz na początku, że a>0 bo lewa strona jest dodatnia, a potem
skorygować rozwiązanie o rozwiązanie nierówności cauchy'ego?
10 maj 21:10
Saizou :
Wystarczyłoby takie coś
| | 1 | |
x∊R\{0} → x4 > 0 i |
| >0, zatem z nierówności Am ≥ Gm |
| | x4 | |
zatem a ≥ 2
10 maj 21:15


