optymalizacja Matfiz: z kwadratowego arkusza tektury o wymiarach 10 na 10 należy wyciąć w rogach kwadraty tak, aby po złożeniu otrzymać otwarte pudełko. Jak należy dobrać długość boku kwadratów, aby objętość pudełka była największa. Chyba źle zrozumiałem zadanie, oznaczyłem bok wyciętego kwadratu jako x a długość krawędzi tektury jako 10−2x i policzyłem objętość sześcianu i wyszła mi sprzeczność, pomoże ktoś?

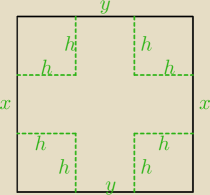
wredulus_pospolitus: pudełko będzie o wymiarach x na y na h

wredulus_pospolitus: od razu widzisz, że x = y ... wyznacz 'h' zależne od 'x' i licz dalej

Matfiz: czyżby długości x i y nie były tej samej długości ?

Matfiz: Dobra teraz widzę jak to ma wyglądać, źle sobie to wyobraziłem wszystko

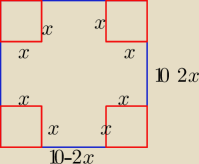
Eta: V= (10−2x)²*x i 10−2x>0 ⇒ x∊(0,5) V^'(x)=0 ............ dokończ

Matfiz: udało się zrobiłem na odwrót boo wyznaczyłem x w zależności od h ale wynik wyszedł dobry długość boku kwadratu = 5/3

Eta: ok

Eta: Po co h? skoro h=x

Matfiz: Nie wiem, taki kaprys miałem

Eta:

Matfiz: A jak mam takie zadanie: Rozpatrujemy wszystkie stożki wpisane w kulę o promieniu 6. Jaka jest wysokość stożka o największej objętości? Od czego tutaj zacząć? Narysowałem przekrój osiowy z którego za wiele nie wynika

ABC: https://zadania.info/d525/4345491