Optymalizacja jokeros2000: Rozpatrujemy trapezy równoramienne ABCD o przekątnej długości 1 i sumie długości podstaw równej x . Zapisz pole trapezu ABCD jako funkcję zmiennej x . Wyznacz dziedzinę tej funkcji i oblicz sumę długości podstaw tego z rozważanych trapezów, którego pole jest największe. Oblicz to największe pole.

fil: wyznacz wysokosc trapezu w zaleznosci od 'x'

jokeros2000: Długość jednego ramienia 1/2 x Przekątna 1 Z pitagorasa wyliczam podstawę Potem liczę wysokość z równości pól Ale potem jest problem z pochodną bo mi wychodzi że x=0

fil: no jak, wyliczasz z pitagorasa wysokosc

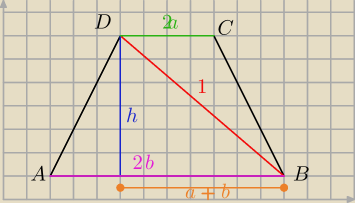
Saizou : 2a+2b=x

	1
a+b=		x
	2

Pitagoras h²+(a+b)²=1

	1
h2=1−		x2
	4

	1
h=√1−		x2
	2

	1		1		1		1
P(x)=		(2a+2b)*√1−		x2=		x√1−		x2
	2		2		2		2

dokończ

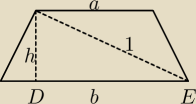
fil: a + b = x

	b − a		a + b		1
|DE| = a +		=		=		x
	2		2		2

jokeros2000: Macie rozwiązanie bo mi wychodzi że maksimum funkcji od pola wynosi 0 i raczej nie powinna być taka odpowiedź

Saizou :

	1		1		1
P(x)=		√x2−		x3 =		√4x2−x3
	2		4		4

Pierwiastek kwadratowy jest funkcją rosnącą i ciągłą, zatem największa wartość funkcja P zostanie osiągnięta, gdy funkcja pod pierwiastkiem osiągnie maksimum. f(x) = 4x²−x³ f'(x)=8x−3x²=0 x(8−3x)=0

	8
x=0 lub x=
	3

f''(x)=8−6x

	8		8
f(		) < 0 zatem w x=		mamy maksimum
	3		3

Bartosz:

	√4x2−x4
Chyba P(x) powinno być
	4

Patryk: To jest to samo Bartosz tylko tutaj sprowadziłeś do wspólnego mianownika wysokość

Chorus : chyba chodzi o ten x stopnia 4−tego

Patryk: W sumie mi też wychodzą dziwne ekstrema: −2 lub 0 lub 2 , żadne nie należy do dziedziny (0; 2)

Chorus : chyba zapomniałeś o pochodnej

Chorus : f'(x) = 8x − 4x³ x= 0 v x= − √2 v x= √2

Patryk: Kto?

Patryk: A kurde, nie spierwiastkowałem