Planimetria jokeros2000: Na bokach AB i AC trójkąta ABC wybrano odpowiednio punkty K i L w ten sposób, że |BK | = |AL | . Punkt D jest środkiem odcinka BC . Przez punkty K i L poprowadzono proste równoległe do AD , które wyznaczyły na boku BC punkty E i F. Wykaż, że jeżeli |BC | = 2|EF| , to |AB | = |AC | .

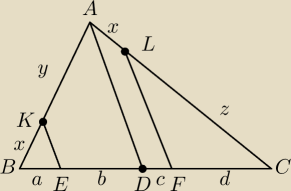
Saizou : 2(a+c)=a+b+c+d (1) a+c=b+d (2) a+b=c+d ==========− c−b = b−c c=b. oraz a=d dokończ

jokeros2000: Jak wykazać że y=z?

Saizou :

x		y
	=		⇒x=y
a		b

x		z
	=		⇒ x=z
c		d

...y=z

jokeros2000: Jakie to twierdzenie jest które zastosowałeś powyżej?

Saizou : tw. Talesa, bodajże z gimnazjum