Punkty Andziula: Odcinek AB gdzie A(1,3) i B(7,−3) jest podstawa trójkata ABC. Oblicz wspólrzedne punktu C tak aby trojkat ABC byl rownoramienny a jego pole bylo rowne 30.

Basia: punkt C musi leżeć na prostej prostopadłej do pr.AB o przechodzącej przez środek odc.AB czyli S=(4;0) P=¹₂*|AB|*|SC| 30 = ¹₂*√6²+(−6)²*|SC| 30 = ¹₂*√36*2*|SC|

	60		10		10√2
|SC| =		=		=		= 5√2
	6√2		√2		2

napisz równanie pr.AB i skorzystaj z wzoru na odległość punktu od prostej

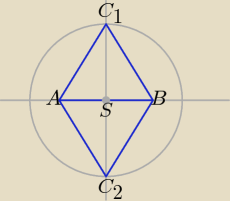
Bogdan: Są 2 rozwiązania. Rysunek zawiera sugestię rozwiazania.

hipek: Podaję plan: 1.oblicz długość podstawy AB 2.mając pole i podstawę oblicz wysokość 3. wyznacz równanie prostej AB 4. wyznacz środek odcinka AB 5. wyznacz równanie prostej prostopadłej do AB i przechodzącej przez środek odcinka AB 6. Szukane współrzędne punktów C spełniają jej warunek 7. wykorzystaj wzór na odległość punktu od prostej 1. AB=√6² + 6²=√72=6√2 2. h=30*2: 6√2=5√2 3. y=−x+4 4. S=(4,0) 5. y=x−4 6. C = (x, x−4) 7. AB: y= −x +4 czyli ogólne równanie: x + y − 4 = 0

[x+x−4−4]
	=5√2 (przepraszam,że zastępuję wartość bezwzględną nawiasem
√12 + 12

kwadratowym, ale nie wiem gdzie go szukać) jeśli pomnożysz stronami przez √2 to otrzymasz [2x − 8] = 10 2x − 8 = 10 lub 2x − 8 = −10 x = 9 lub x = −1 y= 5 y = −5 w ten sposób otrzymasz dwa rozwiązania C=(9,5) lub C=(−1,−5)

Basia: \\\\\\\\\\\\\\\\\\\\\\\\\ a to z shiftem to ||||||||||||||||||||||||||||||||||| ostatni klawisz po prawej, w tym samym rzędzie co A (na małej klawiaturze laptopa)

hipek: Dzięki Basia

Andziula: Hipek rozumiem prawie wszystko mam problemy z punktami 3,4,5 skad to sie pobralo?

Andziula: a i jeszcze skad te 6 w pierszym podpunkcie?