Planimetria dowodowe
Diokona: Dany jest trójkąt ostrokątny równoramienny ABC, w którym AC=BC.
Na bokach zewnątrz tego trójkąta zbudowano kwadraty : ABDE, BCFG oraz ACHJ
Wykaż, że pola trójkątów AHE i BEG są równe.
Kombinuje, kombinuje, ale wykombinować nie moge

10 maj 00:49
a7: cztery sposoby rozwiązań są w informatorze maturalnym str.14−23
10 maj 01:17
wredulus_pospolitus:
zrób rysunek ... zauważ, że są to trójkąty przystające (dwa boki tej samej długości oraz kąt
pomiędzy nimi jest tej samej miary)
10 maj 01:19
a7: to nie są trójkąty przystające
10 maj 01:26
a7:
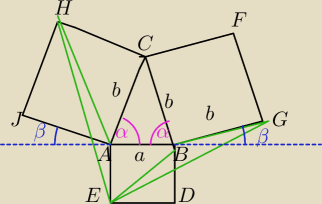
P
BEG=1/2a
√2*b*sin
EBG
P
AHE=1/2b
√2*a*sin
EAH
wystarczy pokazać, że kąt EBG i EAH są równe EBG=45
o+90
o+β , a także EAH=90
o+β+45
o
∡EAH=∡EBG ⇒ sin
∡EAH=sin
∡EBG , wiec P
ΔEAH=P
ΔEBG
c.n.w.
===
10 maj 01:38
Diokona: Dzięki za pomoc

10 maj 13:02

 PBEG=1/2a√2*b*sinEBG
PAHE=1/2b√2*a*sinEAH
wystarczy pokazać, że kąt EBG i EAH są równe EBG=45o+90o+β , a także EAH=90o+β+45o
∡EAH=∡EBG ⇒ sin∡EAH=sin∡EBG , wiec PΔEAH=PΔEBG
c.n.w.
===
PBEG=1/2a√2*b*sinEBG
PAHE=1/2b√2*a*sinEAH
wystarczy pokazać, że kąt EBG i EAH są równe EBG=45o+90o+β , a także EAH=90o+β+45o
∡EAH=∡EBG ⇒ sin∡EAH=sin∡EBG , wiec PΔEAH=PΔEBG
c.n.w.
===
