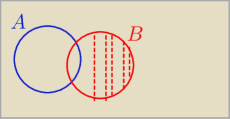
Ilustrowanie zdarzeń w prawdopodobieństwie Shizzer: Zdarzenia A i B są podzbiorami zbioru zdarzeń elementarnych Ω pewnego doświadczenia losowego. Oblicz prawdopodobieństwo zdarzenia A' ∩ B, jeżeli prawdopodobieństwa zdarzeń A i A ∪ B są równe odpowiednio 0,3 i 0,9. Rozwiązanie do tego zadania mam. Chodzi mi tylko o to, żeby zrozumieć jak zaznaczyć na rysunku, które zdarzenia należą do zbioru A', bo nie wiem czy dobrze to rozumiem. Zdarzenia A' to są po prostu zdarzenia ze zbioru zdarzeń Ω, które nie należą do zbioru A? Czyli to są zdarzenia, które zaznaczyłem?

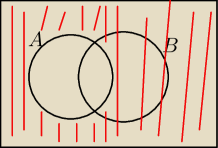
fil: Ja widze zaznaczone P(B) − P(A∩B)

fil:

Shizzer: No i właśnie w książce było zaznaczone tak samo. Nie rozumiem tylko jak to jest możliwe, że te zdarzenia A' wychodzą poza zbiór B. Przecież w zbiorze zdarzeń Ω mamy tylko zdarzenia A i B i myślałem, że tylko w obrębie tych dwóch zbiorów zdarzeń mam operować w doświadczeniu losowym. Jak to działa?

ABC: przecież nie masz w zadaniu napisane że tylko zdarzenia A,B są w Ω

Shizzer: Aaa ok. Czyli zdarzenia A i B są podzbiorami zdarzeń elementarnych Ω, ale nie są JEDYNYMI podzbiorami. Z tego wynika, że istnieją jakieś zbiory innych zdarzeń w zdarzeniach elementarnych Ω, ale ich nie bierzemy pod uwagę tutaj. Więc A' to zdarzenia przeciwne do zdarzeń A więc są to wszystkie zbiory zdarzeń łącznie ze zdarzeniami ze zbioru B. Rozumiem. Dziękuję bardzo!

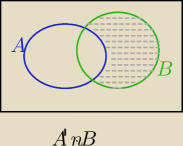
Mila: 1) 20:16 zaznaczony obszar A' 2) P(A)=0.3, P(A∪B)=0.9 P(A'∩B)=P(B\A)=P(B)−P(A∩B

Shizzer: Dokładnie w ten sposób rozwiązałem to zadanie Musiałem tylko zrozumieć jak zilustrować i czym dokładnie są zdarzenia A'. Teraz już rozumiem wszystko co jest mi potrzebne do rozwiązywania tego typu zadań

Mila: