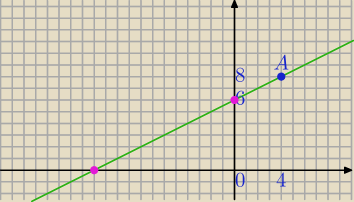
zd: Wyznacz równanie prostej przechodzącej przez punkt A=(4,8) , tworzący wraz z osiami OX i OY w drugiej ćwiartce układu współrzędnych trójkąt prostokątny o polu 36

Eta:

	1
y=		x+6
	2

ABC: zapytam jak trzyletnia dziewczynka : a dlaczego?

Eta:

fil: 6 * 12 = 72

Eta: @fil

	6*12
P=		= 36
	2

WhiskeyTaster: Wskazówka: zauważ, że jedna z przyprostokątnych ma długość |b|, jeśli szukana prosta to y = ax + b. Z kolei druga przyprostokątna to |c| − taka liczba, że f(c) = 0. Stąd już można powiązać to z polem i wyznaczyć co nieco.

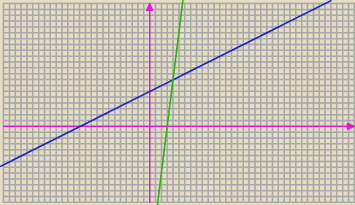
ABC: chodziło mi oto że bez założenia o drugiej ćwiartce zadanie ma dwa rozwiązania , uczniowi trzeba to pokazać żeby mu się utrwaliło

WhiskeyTaster: Trochę nie rozumiem, co masz na myśli W zadaniu jest napisane wyraźnie, że trójkąt jest w drugiej ćwiartce układu współrzędnych.

ABC: chodzi mi o to że mogą na maturze dać bez tego założenia i będą dwa trójkąty wtedy o polu 36 , a ktoś może pomyśleć że zawsze jest tylko jeden

WhiskeyTaster: Ach, to tak. Ale to już moim zdaniem jest błąd tego, kto zadanie rozwiązuje. Trzeba czytać między wierszami

Mila:

	1
PΔ=		*b*|x0|=36, b>0 i x0<0
	2

b*|x₀|=72 y=ax+b i 8=4a+b, a=2−(1/4)b ax₀+b=0

	−b
x0=
	a

	−b
b*|		|=72
	a

	b
b2=72*a⇔b2=72*(2−		) dla a>0
	4

b²+18b−144=0 b=6 lub b=−24∉D

	1		−6
a=		, x0=		=−12
	2		1   2

	1
y=		x+6
	2

=============