analiza olek: Wyznacz ekstrema funkcji (o ile istnieją)

	x2
f(x)=
	x+|2x−5|

Szkolniak:

	10
Dwa minima lokalne: w x=0 oraz x=		.
	3

olek: Jak mam do tego dojść?

HGH: Rozloz funckje na 2 przypadki, w zaleznosci od wartosci bezwzglednej, nastepnie policz pochodna i miejsce zerowe pochodnej.

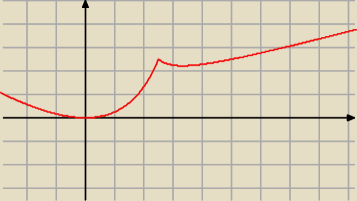
PW: Błąd w myśleniu. Tam gdz\ie "sklejają się" dwie części wykresu, też może być ekstremum.

Olek: Rozpatrzyłem dwie części wykresu, znalazłem dwa ekstrema ale w odpowiedziach jest jeszcze jedno

janek191: x = 2,5

PW: No właśnie. Co gorsza nie można dla tego punktu stosować rachunku różniczkowego (w tym punkcie funkcja nie ma pochodnej). Należy pokazać, że f(2,5) jest ekstremum lokalnym korzystając wprost z definicji ekstremum lokalnego.

Hermes: Raczej takiego zadania na maturce nie będzie jeżeli chodzi o liczenie pochodnych złożonych

PW: Tak, to jest zadanie dla studenta pierwszego roku (a połowa przegapi ten trzeci punkt, chyba ża skorzysta z jakiegoś programu kreślącego wykrey, to może coś skojarzy).