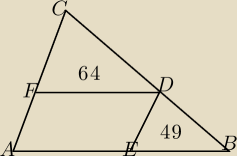
 Oblicz pole trójkąta ABC wiedząc,że pola trójkątów BED i CFE
są odpowiednio równe 49 i 64
Oblicz pole trójkąta ABC wiedząc,że pola trójkątów BED i CFE
są odpowiednio równe 49 i 64
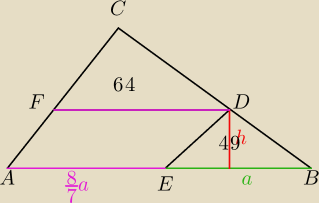
| 64 | 8 | |||
ΔCFD jest podobny do ΔDEB w skali | =( | )2 | ||
| 49 | 7 |
| 8 | 8 | |||
PAEFD= | a*h= | *98=112 | ||
| 7 | 7 |
 P(AEFD)=2√P1*P2
P(AEFD)=2*8*7 =112
P(AEFD)=2√P1*P2
P(AEFD)=2*8*7 =112


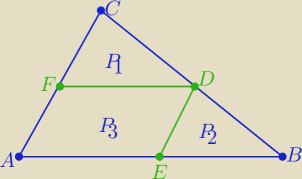 No to dla maturzystów :
Wykazać,że zachodzą takie równości
P=(√P1+√P2)2 i P3=2√P1*P2
No to dla maturzystów :
Wykazać,że zachodzą takie równości
P=(√P1+√P2)2 i P3=2√P1*P2
