równanie stycznej Matfiz: Znajdź równanie prostej, która jest styczna do wykresu funkcji f(x) = −x(x+2) i jednocześnie do wykresu funkcji g(x)=(x−1)² +1. Rozważ wszystkie przypadki. zrobiłem tutaj coś takiego. P(p, f(p)) − współrzędne punktu styczności dla funkcji f f'(x) = −2x−2 f'(p) = −2p−2 y=(−2p−2)(x−p) + (−p² −2p) y= p² −2xp −2x y = x(−2p −2) + p² i analogicznie: H(h, f(h)) − współrzędne punktu styczności dla funkcji g g'(x)=2x−2 g'(h)=2h−2 y=(2h−2)(x−h)+h² −2h+2 y=x(2h−2) −h² +2 i co dalej? Dobrze w ogóle to robię?

f123: f'(x) = −2x − 2 g'(x) = 2x − 2 Styczna do wykresu funkcji f: y = f(x₀)(x − x₀) + f(x₀) Styczna do wykresu funkcji g: y = f(x₁)(x − x₁) + f(x₁) Nastepnie porownujesz wspolrzynniki przy 'x' oraz wyrazy wolne, dostajesz uklad rownanie z dwoma niewiadomymi

f123: Styczna do wykresu funkcji g; y = g'(x₁)(x − x₁) + g(x₁)

f123: i jeszzce poiprawka w wykresie f f'(x₀)(x −......

wredulus_pospolitus: i teraz porównujesz te styczne i sprawdzasz kiedy zachodzi: styczna₁ = styczna₂ czyli kiedy masz:

⎧	(−2p−2) = (2h−2)
⎩	p2 = −h2+2

wredulus_pospolitus: wyliczasz to 'p' , 'h' ... wstawiasz i masz równania (zapewne dwóch) stycznych

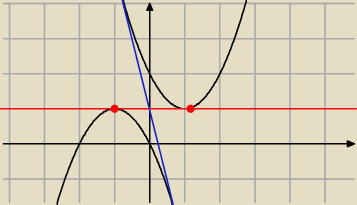
ICSP: szukana prosta : y = ax + b dla pewnych rzeczywistych a i b styczność z wykresem funkcji f y = ax + b y = −x² − 2x ax + b = −x² − 2x x² + (a+2)x + b = 0 Δ = (a+2)² − 4b = 0 styczność z wykresem funkcji g y = ax + b y = x² − 2x + 2 x² − (2 + a)x + 2 − b Δ = (2 + a)² − 4(2 − b) = 0 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− (a+2)² − 4b = 0 (2+a)² − 4(2 − b) = 0 a = 0 i b = 1 a − 4 i b = 1 y = 1 oraz y = −4x + 1

Matfiz: cholerstwo mi coś nie chce wyjść, może mam gdzieś błąd w obliczeniach

Matfiz: dzięki za pomoc, sprawdzę czy nigdzie błędu nie mam w tych obliczeniach

Matfiz: W sumie mi wyszło: dla 'h' h=1 ⋁ h=−1 i współrzędne (1,1) i (−1,5) i dla 'p' p=1 ⋁ p=−1 współrzędne (1,−3) i (−1,1) i teraz skąd mam wiedzieć przez które punkty ma przechodzić styczna? Zgodnie z odpowiedzią jedna styczna musi przechodzić przez punkty (1,1) i (−1,1) a druga styczna przez (−1,5) i (1,−3) ale skąd mam wiedzieć że akurat przez te? Wiem że mogę to z rysunku odczytać