kąt
liceus:
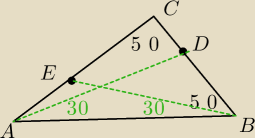
ABC=ACB=50
o
BAD=50
o
ABE=30
o
Oblicz BED=?
Tylko podane są kąty, o odcinkach zielonych nic nie wiadmo tylko to co z rysunku.
8 maj 17:40
Eta:
Popraw treść zadania BAD = ... ?
8 maj 17:50
liceus: Tak 50o mają oba
8 maj 17:53
liceus: i ten trzeci tez
8 maj 17:53
liceus: to zadanie z tematu tw sinsuów
8 maj 17:54
liceus: Nikt nie umie

8 maj 19:12
liceus: up
9 maj 08:42
a7: to w końcu które kąty mają 50o, który trzeci ma 50o?
9 maj 09:02
liceus: Tak jak w poniższej:
ABC=ACB=50o
BAD=50o
ABE=30o
Oblicz BED=?
Na rysunku tam po lewo powinno być 502 przy A.
9 maj 09:18
liceus:
Na rysunku tam po lewo powinno być 50o przy A.
9 maj 09:20
Poprostupatryk: M wychodzi, że miara kąta BED = BAD = 50
o
|DB|=a
coś za łatwe, albo źle zrozumiałem
9 maj 11:02
liceus: Skąd mozesz wyjaśnic

9 maj 12:39
a7:
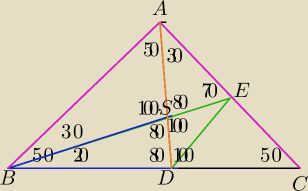
9 maj 14:31
a7: nie wiem jak to zrobić, ale może rysunek pomocniczy się komuś przyda
9 maj 14:31
liceus: up
10 maj 09:08
Poprostupatryk: Zbuduj to twierdzenie dla trójkątów ABD i ADE, które mają wspólny bok BD.
Na przyszłość, staraj się rysować takie rysunki, które jak najbardziej bazują na danych
podanych w zadaniu. Np. wiadomo, że to trójkąt równoramienny bo kąt ABD = kąt ACB
Dobra pokminiłem i zrobiłem tak:
https://zapodaj.net/images/b1877ed975468.jpg
(wiem, że linków lepiej nie wrzucać, no ale nie ma jak własnych grafik).
Najpierw sobie kąty te które mogłem rozpisałem, potem zauważyłem że trójkąty są podobne,
bo mają taki sam kąt 100 stopni oraz ich boki leżą na tych samych prostych.
Więc zapisałem twierdzenie sinusów i proporcje na podobieństwo boków.
Nie wiem czy dobrze ale się starałem.
12 maj 00:02
liceus: Czyli odpowiedzto 40o dobrze rozumiałem?
12 maj 08:08
an: | | a | | a' | |
Poprostupatryk czy tam napisałeś |
| = |
| na jakiej podstawie |
| | b | | b' | |
Jeden ze sposobów to np tak
| sin20 | | sinα | |
| = |
| sin(70+α)=sin70cosα+cos 70sinα |
| sin30 | | sin(70+α) | |
po przekształceniach i korzystając ze wzorów na sin2α i cos2α
otrzymujemy tgα=tg 40
o
α=40
o
12 maj 13:27
Poprostupatryk:
an no wydawało mi się, że trójkąty ABS i DES (z mojego rysunku, gdzie zapomniałem
zaznaczyć wierzchołka S) są podobne, gdzie mają ten sam kat 100 a boki między tym kątem leżą
na tych samych prostych.
Z Twojego rozwiązania nie rozumiem za bardzo skąd to równanie
W twierdzeniu sinusuów musimy chyba porównywać stosunki boków do sinusów kątów
w tym samym trójkącie.
DE i sin30 należy do trójkąta ADE (z mojego rysunku)
ale nie wiem skąd stosunek BD do sin(70+α), nie umiałem tego też
porównać do dwóch innych rysunków.
12 maj 14:31
Poprostupatryk: Czy może nie powinno być: (jeżeli korzystałeś/aś z rysunku a7):
12 maj 14:34
a7: AD=BD
12 maj 14:54
Poprostupatryk: A no fakt, nie zauważyłem. Czyli te trójkąty co powiedziałem, nie są podobne?
12 maj 14:59
a7: nie
12 maj 15:00
a7: podobne są ABS i ADC chyba
12 maj 15:01
an: AD=BD=BS są tam też trójkąty równoramienne i podobne, a ABS i ADS przystające, sporo jak na
jedno zadanie
12 maj 15:11
Iks: Czy mogłoby być takie zadanie na maturze?
12 maj 18:54
a7: | sin20o | | sinα | |
| = |
| |
| 12 | | sin70ocosα+cos70osinα | |
2sin20
o*sin70
ocosα+2sin20
o*cos70
osinα=sinα (zauważamy, że sin70=sin(90−20)=cos20
cos70=cos(90−20)=sin20)
2sin20
ocos20
ocosα+2sin
220
osinα=sinα dzielimy obie strony przez cosinus α
sin40
o+2sin
220
o*tgα=tgα
sin40
o=tgα−2sin
220
otgα
sin40
o=tgα(1−2sin
220
o)
sin40
o=tgα*cos40
o
tgα=tg40
o
α=40
o
===
13 maj 03:50
liceus: Niech F bedzie punktem przeciecia AD oraz BE
| | AE | | AB | |
W △ABE, |
| = |
| |
| | sin30o | | sin70o | |
| | BD | | AB | |
W △ABD, |
| = |
| |
| | sin50o | | sin80o | |
| | AE | | sin80o sin30o | |
|
| = |
| |
| | BD | | sin70o sin50o | |
| | EF | | AE | |
W △AEF, |
| = |
| |
| | sin30o | | sin80o | |
| | DF | | BD | |
W △BDF, |
| = |
| |
| | sin20o | | sin80o | |
| EF | | AE | | sin30o | |
| = |
| |
| = |
| DF | | BD | | sin20o | |
| | sin80o sin30o sin30o | |
= |
| =1 |
| | sin70o sin50o sin20o | |
∠BED=40°
13 maj 08:37
an: Z czego wynika ∠BED=40°

13 maj 18:29
 ABC=ACB=50o
BAD=50o
ABE=30o
Oblicz BED=?
Tylko podane są kąty, o odcinkach zielonych nic nie wiadmo tylko to co z rysunku.
ABC=ACB=50o
BAD=50o
ABE=30o
Oblicz BED=?
Tylko podane są kąty, o odcinkach zielonych nic nie wiadmo tylko to co z rysunku.



