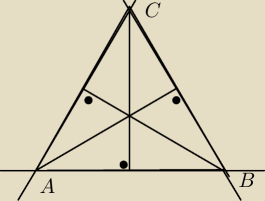
geometria analityczna dzejbi: Podstawa AB trójkąta równoramiennego ABC zawiera się w prostej o równaniu x + 2y −8 = 0 , a ramię AC tego trójkąta zawiera się w prostej o równaniu 7x −11y +119 = 0 . Wyznacz równanie prostej BC wiedząc, że pole trójkąta ABC jest równe 75. P_ABC=75 k: 7x−11y+119=0 −−> k: y=7x−11y+119=0

	1		119
l: x+2y−8=0 −−> l: y=−		x+
	2		11

A:

	1		7		119
−		+4=		x+
	2		11		11

... A=(−6,7) i tu się zaciąłem i nie wiem co dalej liczyć napewno wiem ,że uzależnic jakos wspolrzedne punktu C i skorzystac z odleglosci punktu od prostej tylko kompletnie nie mam pomysłu jak to zrobić

dzejbi:

	1
l:y=−		x+4 oczywiscie
	2

dzejbi: Jak ktos ma pomysl pls help

Szkolniak:

	1		7		119
B=(x1,−		x1+4) oraz C=(x2,		x2+		)
	2		11		11

Może tak o: −> |AC|²=|BC|² −>|AB|²*h²=150², gdzie h²=|SC|², gdzie S to środek odcinka AB. Można stworzyć układ równań z dwoma niewiadomymi, ale nie wiem czy rachunki nie będą wychodzić paskudne.

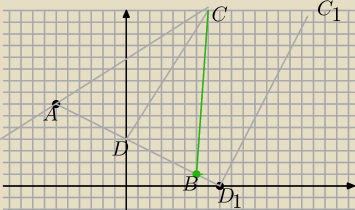
a7: prosta x+2y−8=0 przecina oś OX w punkcie D' (8,0) prosta prostopadła przechodząca przez ten punkt to y=2x−16 punkt C' to punkt przecięcie prostych 7x−11y+119=0 oraz y=−2x−16 C'=(59/3, 70/3) AD'=7√5 odległość punktu C' od prostej AB wynosi 35√5/3 a pole trójkąta AD'C' wynosi 1225/3 i jest podobne do pola trójkąta ADC w skali

	49		7
k2=(1225/3):75=		=(		)2
	9		3

czyli bok AD jest równy 7√5* 3/7=3√5 czyli |AB|=6√5 a |DC|=35√5/3*3/7=5√5 czyli punkt C= (5,14) B=(6,1) D=(0,4) prosta BC=−13x+79 ==============

a7:

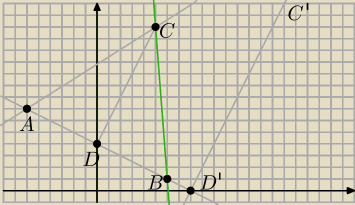
a7: PS. (rysunek "poglądowy")

a7:

a7: II sposób wyznaczamy punkt D=(0,4) wyliczamy AD=3√5 wyznaczamy prostą DC y=2x+4 wyznaczamy punkt C=(5,14) wyznaczamy |DC|=5√5

	75
obliczamy pole trójkąta ADC=37,5=
	2

zauważamy , że jest to połowa naszego trójkąta równoramiennego wyznaczamy punkt B=(6,1) wyznaczamy prostą BC: y=−13x+79 ==============

dzejbi: a7 wszystko się zgadza znaleźliśmy jedną prostą ale istnieje jeszcze podobno druga y=−13x+−221

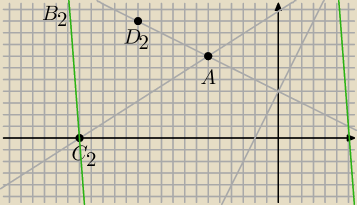
a7: wyznaczamy D₂=(−12,10) AD₂=3P{5} C₂= (−17,0) C₂D₂=5√5 lub od razu B₂=(−18,12) prosta B₂C₂: y=−13x−221 ====================

Mila: a7, rozwiązałam najpierw, tak jak Ty, ale znalazłam inny sposób na wyznaczenie wsp. punktu C. Jutro napiszę, jeśli jesteś zainteresowana.

a7: ja chętnie

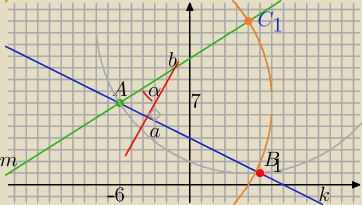
Mila: |AC|=|BC|=b k: x + 2y −8 = 0 ,

	7		119
m: 7x −11y +119 = 0 ⇔y=		x+
	11		11

A=(−6,7) 1) Kąt między m i prostopadłą y=2x+b do AB

	7   2−   11		3
tgα=		=		, α− kąt ostry
	7   1+2*   11		5

	3		5
stąd sinα=		cosα⇔cosα=		i sin α=U{3}{√34
	5		√34

	15
2sinα*cosα=sin2α=		− sinus kąta między ramionami
	17

	1		15
PΔ=75=		b2*		⇔b2=170
	2		17

2) Współrzędne punktu C: (x+6)²+(y−7)²=170 i y=(7/11)x+(119/11)⇔ C₁=(5,14) i C₂=(−17,0) 3) współrzędne punktu B₁

	1
(x−5)2+(y−14)2=170 i y=−		x+4
	2

B₁=(6,1) Współrzędne B ₂ za pomocą symetrii środkowej względem p. A ( najprościej) albo tak jak B₁, ale okrąg ośrodku C₂ 4) Teraz równania prostych

a7: (warto znać i ten sposób, choć sposób z 6:34 trochę łatwiejszy i trudniej się pomylić)

a7: PS. Dzięki

Mila: Tak, masz rację, od razu zrobiłam tak , jak masz 6:34, dane tak dobrane , że natychmiast jest rozwiązanie, w innym przypadku może być inaczej.

a7: no tak