geometria
salamandra: Jeden z wierzchołków trojkata równobocznego leży na wierzchołku paraboli y=x2−4x, a pozostałe
leżą na jej ramionach
a) wyznacz współrzędne wierzchołków trojkata
b) oblicz objętość bryły powstałej przez obrót tego trojkata dookoła prostej y=−4
Na razie mam problem z a)−
wyznaczyłem A=(2, −4) = W
B=(2−x, x2−4x)
C=(2+x, x2−4x)
AB=AC=BC ale wychodzą mi z tego same równoważności
8 maj 14:34
Jerzy:
Pewnie brakuje dodatkowego warunku w treści zadania.
8 maj 14:42
ite: Nie wykorzystałeś informacji, że to trójkąt równoboczny.
8 maj 14:55
Jerzy:
Przecież porównuje boki.
8 maj 15:00
ICSP: ile wynoszą
|BC| i |AB| ?
8 maj 15:06
ABC:
jeżeli pierwsza współrzędna 2−x , to druga (2−x)2−4(2−x)=4−4x+x2−8+4x=x2−4
8 maj 15:07
ite: Można zauważyć, że kąt pomiędzy prostymi AB i BC wynosi 60o
i prosta x=2 jest jego dwusieczną.
To daje informację, pod jakimi kątami do osi OX są nachylone proste AB i BC,
a współrzędne punktu A znamy.
Mając równania prostych AB i BC, szukamy ich punktów wspólnych z parabolą (czyli B i C).
8 maj 15:18
ite: *w każdym miejscu miało być napisane:
proste AB i AC (A to wierzchołek paraboli)
8 maj 15:21
Jiraya:
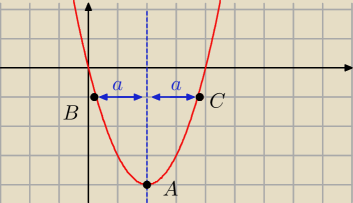
A=(2, −4)
Niech C = (x, x
2−4x) wówczas (założenie x > 2)
a = x − 2
x
b = x − 2a = x − 2(x−2) = 4 − x
B = (4−x, x
2−4x)
|AC| = |BC| |
2
(x−2)
2 + (x
2−4x+4)
2 = (x−(4−x))
2 + (x
2−4x−(x
2−4x))
2
(x−2)
2 + (x−2)
4 = (2x−4)
2
(x−2)
2(1+(x−2)
2) = 4(x−2)
2
1+(x−2)
2 = 4
(x−2)
2 = 3 |
√
|x−2| =
√3
x−2 =
√3 lub x−2=−
√2
x = 2+
√3 lub x=2−
√2 < 2
(2+
√3)
2−4(2+
√3)=7+4
√3−8−4
√3=−1
B = (2−
√3, −1)
C = (2+
√3, −1)
8 maj 15:51
salamandra: Dzięki. @ite tez mi coś zaświtało na początku z tym nachyleniem, ale nie wiedziałem jak się za
to zabrać
8 maj 16:05
Mila:
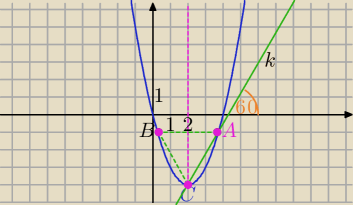
y=x
2−4x
C=(2,−4)
1) a=tg60
o − wsp. kierunkowy prostej
k: y=
√3x+b i −4=2
√3+b, b=−4−2
√3
y=
√3x−4−2
√3 ,
2) Punkt przecięcia z parabolą
√3x−4−2
√3=x
2−4x
x
2−(4+
√3)x+4+2
√3=0
stąd x
1=2 i y=−4) lub x
2=2+
√3 i y=−1
C=(2,−4) i A=(2+
√3,−1)
3) rozwiązujesz równanie: x
2−4x=−1⇒otrzymujesz wsp. punktu B
albo translacja punktu A o odpowiedni wektor
8 maj 18:15
 A=(2, −4)
Niech C = (x, x2−4x) wówczas (założenie x > 2)
a = x − 2
xb = x − 2a = x − 2(x−2) = 4 − x
B = (4−x, x2−4x)
|AC| = |BC| |2
(x−2)2 + (x2−4x+4)2 = (x−(4−x))2 + (x2−4x−(x2−4x))2
(x−2)2 + (x−2)4 = (2x−4)2
(x−2)2(1+(x−2)2) = 4(x−2)2
1+(x−2)2 = 4
(x−2)2 = 3 |√
|x−2| = √3
x−2 = √3 lub x−2=−√2
x = 2+√3 lub x=2−√2 < 2
(2+√3)2−4(2+√3)=7+4√3−8−4√3=−1
B = (2−√3, −1)
C = (2+√3, −1)
A=(2, −4)
Niech C = (x, x2−4x) wówczas (założenie x > 2)
a = x − 2
xb = x − 2a = x − 2(x−2) = 4 − x
B = (4−x, x2−4x)
|AC| = |BC| |2
(x−2)2 + (x2−4x+4)2 = (x−(4−x))2 + (x2−4x−(x2−4x))2
(x−2)2 + (x−2)4 = (2x−4)2
(x−2)2(1+(x−2)2) = 4(x−2)2
1+(x−2)2 = 4
(x−2)2 = 3 |√
|x−2| = √3
x−2 = √3 lub x−2=−√2
x = 2+√3 lub x=2−√2 < 2
(2+√3)2−4(2+√3)=7+4√3−8−4√3=−1
B = (2−√3, −1)
C = (2+√3, −1)
 y=x2−4x
C=(2,−4)
1) a=tg60o − wsp. kierunkowy prostej
k: y=√3x+b i −4=2√3+b, b=−4−2√3
y=√3x−4−2√3 ,
2) Punkt przecięcia z parabolą
√3x−4−2√3=x2−4x
x2−(4+√3)x+4+2√3=0
stąd x1=2 i y=−4) lub x2=2+√3 i y=−1
C=(2,−4) i A=(2+√3,−1)
3) rozwiązujesz równanie: x2−4x=−1⇒otrzymujesz wsp. punktu B
albo translacja punktu A o odpowiedni wektor
y=x2−4x
C=(2,−4)
1) a=tg60o − wsp. kierunkowy prostej
k: y=√3x+b i −4=2√3+b, b=−4−2√3
y=√3x−4−2√3 ,
2) Punkt przecięcia z parabolą
√3x−4−2√3=x2−4x
x2−(4+√3)x+4+2√3=0
stąd x1=2 i y=−4) lub x2=2+√3 i y=−1
C=(2,−4) i A=(2+√3,−1)
3) rozwiązujesz równanie: x2−4x=−1⇒otrzymujesz wsp. punktu B
albo translacja punktu A o odpowiedni wektor