geometria analityczna,okrag wpisany w trojkat
dzejbi: Wyznacz równanie okręgu wpisanego w trójkąt o wierzchołkach A = (−1,3), B = (−5,6), C = (−9,3).
Cześć, mam problem z tym zadankiem i nie wiem czy błąd jest po stronie obliczeniowej czy
rozumowej.
|AB|=
√(−5+1)2+(6−9)2=
√16+9=5
|BC|=
√(−5+9)2+(6−3)2=
√16+9=5
|AC|=
√(−9+1)2+(3−3)2=
√64+0=8
|AB|=|BC| −−> trójkąt równoramienny
h=3 z pitagorasa (h
2+4
2=5
) (h
2+16=25) −−> h
2=9 −−−> h=3
2p=18 −−> p=9
pr
AC: y=3
| | −1−3 | | 3+3 | |
SAC(środek boku AC) −−>SAC=( |
| , |
| )−−> SAC=(−2,3) |
| | 2 | | 2 | |
pr BS
AC: y=−x+1
no to środek okręgu leży na prostej y=−x+1 −−> S=(x,−x+1)
więc odległość środka okręgu od prostej AC jest równa odległości środka okręgu od prostej AB
d(S,pr
AC)=d(S,pr
AB)
pr
AC: y−3=0
| | 3 | | 9 | |
prAB: − |
| x−y+ |
| =0 || *(−4) |
| | 4 | | 4 | |
pr
AB: 3x+4y−9=0
| |0*x+1(−x+1)−3| | | 3*x+4(−x+1)−9| | |
| = |
| |
| √02+12 | | √32+42 | |
|−5x−10|=|−x−5|
−5x−10=−x−5 v −5x−10=x+5
−4x=5 v −6x=15
no i jak podstawiam to nic nie wychodzi bo wynik to:
starałem się to starannie robić i nie wiem gdzie jest problem może gdzieś się pomyliłem z
prostą ,może zły tok rozumowania
proszę o pomoc!
7 maj 14:45
f123: |AB| zle obliczyles
7 maj 14:46
f123: A nie, zly zapis, ale wynik taki sam
7 maj 14:47
dzejbi:
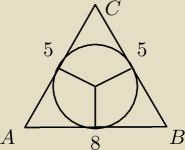
7 maj 14:48
dzejbi: ojj rysunek odwrotnie boki ale wiadomo o co chodzi

7 maj 14:49
dzejbi: a no tam powinno być 6−3 fakt ale to już jak z kartki przepisywałem to pomyliłem 3 z 9
7 maj 14:50
f123: Czemu jak liczysz srodek wspolrzedne srodka odcinka AC to 1sza wszpolrzedna to "−1 − 3"

7 maj 14:56
f123: | | −1 + (−9) | | 3 + 3 | |
SrodekAC = ( |
| , |
| ) => (−5, 3) |
| | 2 | | 2 | |
7 maj 14:59
dzejbi: faktycznie , moje niedopatrzenie
7 maj 15:05
jc:
A=(−1,3), B = (−5,6), C = (−9,3).
| | BC | | CA | | AB | |
S= |
| A + |
| B + |
| C |
| | AB+BC+CA | | AB+BC+CA | | AB+BC+CA | |
| | 5 | | 8 | | 5 | |
S= |
| (−1,3) + |
| (−5,6) + |
| (−9,3) = (−5, 13/3) |
| | 18 | | 18 | | 18 | |
o ile dobrze podstawiłem.
7 maj 15:05
Poprostupatryk: Skąd ten wzór jc?
| | BC | |
S = |
| A+... |
| | AB + BC + CA | |
7 maj 16:05
dzejbi: mógłby ktoś pokazać rozwiązanie na poziomie liceum?
7 maj 16:28
jc: Przecież masz ten sam wynik: (−5, 13/3).
7 maj 16:39
dzejbi: znaczy nie znam tego wzoru a z mojego mi wciaz nie wychodzi
7 maj 16:50
dzejbi: Jak ktoś wie to chętnie zobacze odp :v
7 maj 19:28
jc:
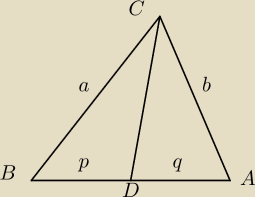
Na rysunku trójkąt przecięty dwusieczną.
Znamy a, b, c=p+q. Ile wynosi p, a ile q?
7 maj 19:40
Mila:
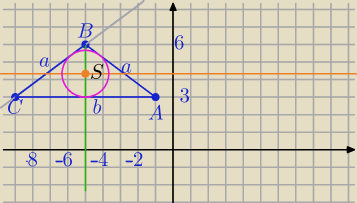
A = (−1,3), B = (−5,6), C = (−9,3).
1) a=5, b=8
2) Dwusieczne:
x=−5 dwusieczna ∡ABC
| | 3 | |
Prosta BC: y=ax+b, a = |
| |
| | 4 | |
3x−4y+39=0
S=(−5,n) − środek okręgu
odległość środka okręgu od prostej AC jest równa r
| 4 | |
| *5=|−15−4n+39| i 3<n<6 |
| 3 | |
=========
7 maj 21:29
jc: Mila, ciekawostką jest, że mamy prosty wzór. na dodatek łatwy do uzyskania.
A skąd wiem? Pół roku temu było na forum podobne zadanie,
tyle że trójkąt był raczej przypadkowy.
7 maj 22:00
Mila:
Tak, JC, ale ja nie zapamiętałam. Teraz sobie przypomniałam, że jest.
W tym zadaniu jest "prosty" trójkąt do liczenia, ale w innym przypadku może być sporo
rachunków.
Przypomnę sobie w trochę innej postaci niż Ty napisałeś.
7 maj 22:06
Mila:
Współrzędne środka okręgu wpisanego w trójkąt o danych wsp. wierzchołków.
A = (−1,3), B = (−5,6), C = (−9,3)
a=5, b=8, c=5
5+8+5=18
| | 5*(−1)+8*(−5)+5*(−9 | | −5−40−45 | |
xs= |
| = |
| =−5 |
| | 18 | | 18 | |
| | 5*3+8*6+5*3 | | 78 | | 13 | |
ys= |
| = |
| = |
| |
| | 18 | | 18 | | 3 | |
7 maj 22:45



 Na rysunku trójkąt przecięty dwusieczną.
Znamy a, b, c=p+q. Ile wynosi p, a ile q?
Na rysunku trójkąt przecięty dwusieczną.
Znamy a, b, c=p+q. Ile wynosi p, a ile q?
 A = (−1,3), B = (−5,6), C = (−9,3).
1) a=5, b=8
A = (−1,3), B = (−5,6), C = (−9,3).
1) a=5, b=8