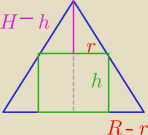
Zadanie optymalizacyjne bez danych w treści Shizzer: W stożek, którego przekrojem osiowym jest trójkąt równoboczny, wpisano walec o największej objętości. Oblicz stosunek promienia podstawy walca do promienia podstawy stożka. Widzę, że mogę tutaj skorzystać z podobieństwa trójkątów, ale gubię się przy tego typu zadaniach. Skoro w ogóle nie mam podanych danych w treści to mam sam przyjąć, która zmienną jest tutaj daną? Nie wiem czy kiedykolwiek zrozumiem jak mam robić takie zadania, ale dobrze byłoby je rozumieć na maturę

wredulus_pospolitus: h ∊ (0 ; H) r ∊ (0 ; r)

h		H−h		H(R−r)
	=		−> hr = RH − rH − Rh + rh −−> Rh = H(R−r) −−−> h =
R−r		r		R

	H(R−r)
Vwalca = πr2*h = πr2*
	R

szukasz maksimum ... wyznaczasz V_{max walca}

	1
Vstożka =		πR2*H
	3

liczysz stosunek objętości

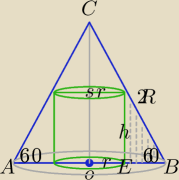
Mila: Ustalasz, że dany jest bok Δrównobocznego a=2R. V=πr²*h 1) |AB|=2R, |OB|=|OA|=R |EB|=R−r

	h
tg60=		⇔h=√3*(R−r)
	(R−r)

2) V(r)=πr²*√3(R−r)=√3π*(R*r³−r²), r∊(0,R) i liczysz

Shizzer: Ok, czyli w takim zadaniu sam sobie mogę ustalić daną. Niestety nie wiedziałbym, którą z nich wybrać dlatego zapytam. Czym mam się kierować przy wyborze danej w tego typu zadaniach? Dlaczego na przykład tutaj daną jest a=2R, a nie np. r? To chciałbym zrozumieć

wredulus_pospolitus: przeważnie wyznacza się tę której później nie trzeba pierwiastkować bądź podnosić do potęgi więc dlatego preferuje się wyznaczyć 'h' a nie 'r'

wredulus_pospolitus: po prostu później jest 'mniej zabawy' z tym A ja oczywiście nie skorzystałem z tego, że jest to trójkąt równoboczny

wredulus_pospolitus: A 'dane' masz wymiary które są stałe i niezmienne −−− czyt. wymiary stożka Bo to walca chcesz 'optymalizować' (czyli wartości r i h są zmiennymi przy jakiś stałych R i H).

Mila: Podano, że przekrojem jest Δ równoboczny, możesz napisać, bok Δ jest równy a.

	1
Wtedy promień podstawy stożka R=		a i możesz sobie dalej liczyć.
	2

Wszystkie Δrównoboczne są podobne, zatem stosunek promieni będzie zawsze w takim zadaniu taki sam. W moim sposobie od razu otrzymasz to co masz podać w odpowiedzi, a obliczenia są uproszczone. Wredulus podał sposób bardziej ogólny, jeśli przekrojem jest Δrównoramienny.

Shizzer: Wszystko jasne. Bardzo Wam dziękuję

Shizzer: A czy funkcja V(r) nie powinna być czasem zapisana tak: V(r) = √3π*(R*r²−r³)?

Bleee: Powinna byc

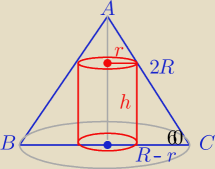
Shizzer: Wrzucę rozwiązanie, może ktoś kiedyś skorzysta: Korzystając z własności trójkąta równobocznego: |AC| = 2R Optymalizujemy walec więc r i h są zmiennymi. Wpisujemy walec w stożek opisany stałymi zatem R i H stożka są dane. Wielkość, którą optymalizujemy: V = πr² * h Uzależniam h od r dzięki temu objętość walca będzie funkcją jednej zmiennej zależną od r:

	h
tg60o =		⇒ h = √3 * (R − r)
	R − r

V jako funkcja jednej zmiennej: V(r) = πr² * √3 * (R − r) = √3π * (Rr² − r³) Wyznaczam dla jakiego r objętość walca będzie maksymalna: V'(r) = √3 * (2Rr − 3r²), gdzie r ∊ (0, R) V'(r) = 0 2R − 3r² = 0 r(2R − 3r) = 0

	2
r = 0 ∨ r =		R
	3

	2
V'(r) > 0 dla r ∊ (0,		R)
	3

	2
V'(r) < 0 dla r ∊ (		R, R)
	3

	2
Zatem Vmax dla r =		R
	3

Znając r obliczam stosunek promieni:

2   R 3		2
	=
R		3

Mila: V(r) jak napisałeś

Hermes: Czemu w tym zadaniu pod optymalizacje bierzemy 2 zmienne R oraz r?

Shizzer: R jest w tym zadaniu daną. Można ją traktować na przykład jak liczbę 5. W optymalizacji objętości walca bierze udział tylko r

Hermes: A mam jeszcze takie stanie, gdzie się podziało "π" w funkcji optymalizowanej?

Shizzer: Zgubiłem po drodze. Pochodna powinna wyglądać w ten sposób: V'(r) = √3π * (2Rr − 3r2) Przy liczeniu ekstremów lokalnych funkcji V to π tak czy inaczej się skróci.

wredulus_pospolitus: Hermes −−− π (jak również √3) nie mają żadnego wpływu na samą optymalizację ... można równie dobrze je pominąć przy liczeniu pochodnej