Napisać równanie prostej prostopadłej do prostej l przechodzącej przez punkt M Liczba_π:

	x+1		z−2
Napisać równania prostej prostopadłej do prostej l :		= −y =		, przechodzącej
	2		3

przez punkt M(2,3,1) Wyznaczam punkt P leżący na prostej l i jej wektor kierunkowy P(−1, 0, 2) v=[2, −1, 3] Czy mogę wziąć jakikolwiek wektor prostopadły do wektora v i przyjąć go jako wektor kierunkowy prostej k⊥l gdzie M∊k ? np. u=[2, 7, 1] lub n=[1, −1, −1]

	x−2		y−3
k:		=		= z−1 lub k: x−2= −y+3=1−z
	2		7

Czy te dwie proste powyżej są tą samą prostą ⊥ do prostej l i przechodzącą przez punkt M ?

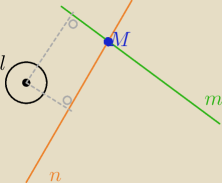
Des: Te dwie proste przez Ciebie wymienione spełniają warunki zadania, wektor kierunkowy każdej z nich jest prostopadły do wektora v i obie przechodzą przez punkt M, mimo, że są to dwie różne prsote. Jak widać wcale nie muszą się one przecinać. (Prosta ' l ' biegnie przed i za ekran)