monotoniczność
salamandra: | | x2+3 | |
Wyznacz maksymalne przedziały monotoniczności funkcji f(x ) = |
| |
| | x2−1 | |
D:R \ {−1,1}
| | 2x(x2−1)−(x2+3)2x | | −8x | |
f'(x)= |
| =U{2x3−2x−2x3−6x}{(x2−1)2= |
| |
| | (x2−1)2 | | (x2−1)2 | |
f'(x)=0 ⇔ −8x=0 ⇒ x=0
I tutaj mam dylemat, bo wiele razy widziałem tu dyskusje nt. funkcji wymiernej − kiedy można
pisać np. że funkcja rośnie w R \ {x}, a kiedy trzeba napisać, że (−
∞;x)U(x;+
∞)
Dla bezpieczeństwa tu napisałem, że funkcja rośnie w (−
∞;−1)U(−1;0) , a funkcja maleje w
(0;1)U(1;+
∞)
czy zapis: funkcja rośnie w (−
∞;0) \ {−1}
funkcja maleje w (0;+
∞) \ {1} będzie równoważny?
6 maj 12:14
wredulus_pospolitus:
zanim zrobisz pochodną ... przekształć funkcję:
| | x2 + 3 | | x2 − 1 + 4 | | 4 | |
f(x) = |
| = |
| = 1 + |
| |
| | x2−1 | | x2−1 | | x2−1 | |
'ładniejsza' pochodna wychodzi

6 maj 12:16
wredulus_pospolitus:
a raczej ... 'łatwiejsza do policzenia'
6 maj 12:16
Jerzy:
| | 1 | |
Np: funkcja f(x) = |
| jest malejąca w przedziałach (−∞,0) oraz (0,∞) , a nie w całej |
| | x | |
dziedzinie.
6 maj 12:16
ICSP: jakim cudem funkcja ma rosnąć w
x ∊ (− ∞ ; −1) ∪ (−1 ; 0)
skoro dla x < −1 wartości ma dodatnie a dla −1 < x < 0 wartości ma ujemne?
Wiesz w ogóle co oznacza, ze funkcja jest rosnąca?
6 maj 12:17
Jerzy:
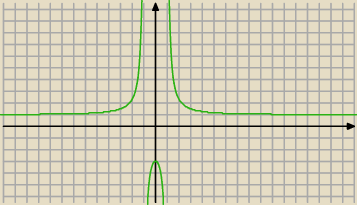
6 maj 12:20
wredulus_pospolitus:
zapis:
f↗ w (−∞, 0) \ {−1} nie jest równoznaczny z zapisem
f↗ w (−∞, −1) oraz w (−1,0)
ze względu na to asymptotę pionową x = −1
jakbyś policzył granice dla x−> −1 to byś zauważył (co można także wydedukować z
monotoniczności funkcji), że:
limx−> −1− f(x) = + ∞
limx−> −1+ f(x) = − ∞
związku z tym ... śmiem twierdzić, że
f(−1.000000000001) > f(−0.99999999999)
co oznacza, że nie jest prawdą, że funkcja rośnie na przedziale (−1.000000001 ; −0.99999999) \
{−1}
6 maj 12:21
wredulus_pospolitus:
Z tego powodu NIGDY nie podaje się (przy monotoniczności) sumy przedziałów, tylko je się
rozdziela i pisze, że funkcja (osobno) rośnie w każdym z nich.
Jedyny wyjątek jaki można zrobić, to w momencie gdy mamy z f'(x) jakiś punkt przegięcia (np.
f(x) = x3 −> f'(x) = 3x2 −−−> x = 0 jest punktem przegięcia) ... wtedy można połączyć
przedziały i wrzucić punkt przegięcie
6 maj 12:23
salamandra: @ICSP, a co niby robi w przedziale (−1;0)?
6 maj 12:24
wredulus_pospolitus:
salamndra
funkcja rośnie w przedziale (−∞ ; −1)
funkcja rośnie w przedziale (−1 ; 0)
ale funkcja NIE ROŚNIE w przedziale (−∞;−1) u (−1 ; 0)
co Ci pokazałem o 12:21
6 maj 12:25
salamandra: | | 1 | |
czyli "u" oznaczałoby, że funkcja przyjmuje wartości większe dla np. − |
| , niż dla −2? |
| | 2 | |
6 maj 12:26
wredulus_pospolitus:
dokładnie
6 maj 12:27
wredulus_pospolitus:
bo zapis (−∞;−1) u (−1 ; 0) oznacza, że traktuje to jako JEDEN zbiór i w całości w tym
zbiorze zachodzi:
x1 < x2 ⇒ f(x1) < f(x2) (co jest definicją funkcji rosnącej)
6 maj 12:28
wredulus_pospolitus:
dlatego zapis:
funkcja rośnie w (−∞;−1) u (−1 ; 0)
oraz
funkcja rośnie w (−∞;−1), w (−1 ; 0)
to dwa całkowicie różne zapisy −−− pierwszy w 99% przypadków będzie błędny ... drugi jest
poprawny (przy założeniu że poprawnie policzona pochodna i takie tam)
6 maj 12:29
salamandra: własnie o to było moje docelowe pytanie − myślałem, że takie coś tylko ma miejsce, gdy napiszę
że rośnie w R \ {−1}
6 maj 12:32
wredulus_pospolitus:
No to już wiesz, że nie.
'zsumować' przedziały mógłbyś np. dla takiej funkcji:
Funkcja taka będzie rosnąca w przedziale R \ {−1 ; 1}
albo jak wolisz (−
∞ ; −1) u (−1 ; 1) u (1 ; +
∞)
6 maj 12:35
salamandra: A dla bezpieczeństwa mógłbym rozbić na dwa przedziały ze spójnikiem „w”?
6 maj 12:36
ABC:
najbezpieczniej pisz : funkcja jest rosnąca w każdym z przedziałów , i oddzielaj przecinkiem
6 maj 12:39
wredulus_pospolitus:
Jeżeli w treści masz: 'sprawdź monotoniczność' lub 'podaj przedziały monotoniczności' ...
tak
Jeżeli jednak treść zadania jest taka jak tutaj: 'podaj MAKSYMALNE przedziały monotoniczności'
to trzeba podać maksymalne możliwe przedziały i wtedy zapis:
rośnie w (−∞ ; −1), w (−1 ; 1), w (1 ; +∞)
no raczej poprawną odpowiedzią by nie było −−−− ale mocno wątpię by coś takiego trafiło się
na maturze ( na maturze nie ma zadań 'podchwytliwych' )
6 maj 12:39

