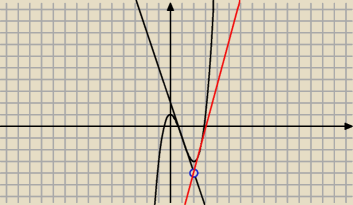
Równania stycznych do wykresu Maciek : Napisz równania stycznych do wykresu funkcji f danej wzorem f(x)=x³ − 3x² + 1 na których leży punkt p (2,−4)

wredulus_pospolitus: krok 1: ogólna postać stycznej do f(x) w punkcie K (a, f(a)) krok 2: 'wrzucasz' współrzędne punktu P do wzoru ogólnego stycznej ... wyznaczasz dla jakich wartości 'a' równanie jest spełnione krok 3: wyznaczasz ostateczne postaci stycznych do funkcji f(x) korzystając z wyliczonych 'a'

Maciek : Mógłbyś rozpisać ostatni krok ? Narazie wyszło mi ze a =1 lub a = 5/2

piotr: f'(x)=3x² − 6x równanie stycznej w punkcie (x₀, f(x₀)): y − f(x₀) = f'(x₀)(x − x₀) ⇒ y − (x₀³ − 3x₀² + 1) = (3x₀² − 6x₀)(x − x₀) prosta ta przechodzi przez punkt p(2, −4) ⇒ −4 − (x₀³ − 3x₀² + 1) = (3x₀² − 6x₀)(2 − x₀) ⇒ x₀ = 1 ∨ x₀ = 5/2 ⇒ stąd dwie styczne: 1+y = −3 (−1+x) lub 17/8+y = 15/4 (−(5/2)+x)

Maciek : Dzięki!