Nie wiem co nawet
Adi: W trójkąt równoramienny o kącie między ramionami równym 2α, gdzie α∊(0; π/2)
wpisano półokrąg o promieniu R w ten sposób, że jego średnica leży na podstawie
trójkąta. Funkcja f(α) wyraża obwód koła wpisanego w ten trójkąt w zależności od kąta α.
Wskaż zdania prawdziwe.
a) Dla każdego α ∈(0; π/2) zachodzi nierówność f (α) > πR.
b) Dla pewnego α ∈(0; π/2)funkcja f przyjmuje wartość największą.
c) Istnieje α∈(0; π/2) takie, że f (α)≤ πR
d) Funkcja f jest monotoniczna w przedziale (0; π/2)
Wie ktoś o co chodzi w tym zadaniu, jak się zabrać za to w ogóle, albo czy zna ktoś jakieś
podobne zadanie które jest rozwiązane, tak żebym mógł zrozumieć o co chodzi

5 maj 19:49
a7:
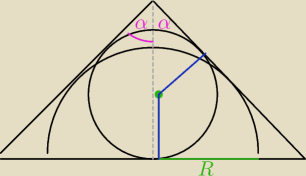
najpierw pomocniczy rysunek
5 maj 20:09
a7:
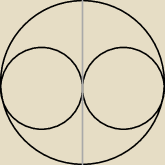
następnie wiadomo,że np. dwa okręgi o tym samym promieniu wpisane w okrąg będą miały w sumie tę
| | R | | R | |
samą długość równą 2πR=2π |
| +2π |
| czyli jeden okrąg będzie miał połowę tej długości |
| | 2 | | 2 | |
równą πR
następnie w naszym przykładzie okrąg będzie zawsze "wystawał" ponad półokrąg gdyż trójkąt
równoramienny w treści zadania to "gwarantuje" (nie możliwe jest aby ramiona były równoległe
do podstawy)
czyli a)prawda (wg mnie)
5 maj 20:14
a7: c) w związku z tym c) nieprawda
5 maj 20:16
anx: a czy b) nie jest zagwarantowane przypadkiem z treści zadania. Wszak skoro kąt α się zmienia to
funkcja f(α) na pewno nie będzie stała, poza tym mamy maksymalny przedział wartości które może
przyjąc α, a z połączenia tych dwóch warunków (tego że nie jest stała i jest ograniczona) nie
wnioskujemy że ma na pewno max oraz min?
5 maj 20:31
a7: @anx jeśli chodzi o b) to wydaje się to logiczne, ale nie wiem
@Adi czy rozumiesz już o co chodzi w zadaniu?
5 maj 20:40
Adi: Rozumiem ale nie wiem jak do tego podejść zbyt. Chociaż już sporo mi się rozjaśniło
5 maj 21:00
a7:
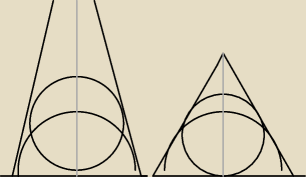
wydaje się, że im mniejsza α tym większy okrąg, przynajmniej do pewnego momentu
5 maj 21:17
a7:
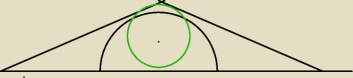
5 maj 21:19
anx: Myślę, że d jest prawdziwe bo im większę a (w przedziale (0, π/2) tym mniejszy jest obwód
okręgu wpisanego w trójkąt −−> funkcja jest malejąca −−> funkcja jest monotoniczna
5 maj 21:24
anx: Czyli a) prawda (raczej), więc c to nieprawda oraz b i d są prawdziwe
5 maj 21:25
a7: a) prawda, gdyż jak napisałam wcześniej (20:14) okrąg zawsze będzie wystawał ponad półokrąg
czyli będzie miał promień większy niż pół promienia półokręgu
| | R | |
gdyby miał promień równy r= |
| to jego obwód byłby dokładnie 2πR/2=πR, tak nie jest więc |
| | 2 | |
jego promień i obwód zawsze są co najmniej ciut większe
5 maj 21:34

 najpierw pomocniczy rysunek
najpierw pomocniczy rysunek
 następnie wiadomo,że np. dwa okręgi o tym samym promieniu wpisane w okrąg będą miały w sumie tę
następnie wiadomo,że np. dwa okręgi o tym samym promieniu wpisane w okrąg będą miały w sumie tę
 wydaje się, że im mniejsza α tym większy okrąg, przynajmniej do pewnego momentu
wydaje się, że im mniejsza α tym większy okrąg, przynajmniej do pewnego momentu
