 Wyznacz równanie prostej przechodzącej przez punkt A = (−2, −1) i przecinającej ujemne
półosie układu współrzędnych w takich punktach, których suma odległości od początku
układu współrzędnych jest najmniejsza.
Coś zrobiłem źle, ale nie wiem gdzie popełniłem błąd. Gdyby ktoś mógł mi go wskazać byłbym
wdzięczny.
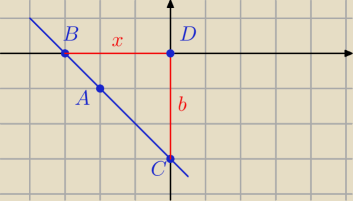
A = (−2, −1)
B = (x, 0)
C = (0, b)
D = (0, 0)
Suma odległości punktów B i C od początku układu współrzędnych:
S = x + b
1. Uzależniam b od a:
−1 = −2a + b ⇒ b = 2a − 1
C = (0, 2a − 1)
S = x + 2a − 1
2. Uzależniam x od a:
ax + 2a − 1 = 0
ax = −2a + 1
Wyznacz równanie prostej przechodzącej przez punkt A = (−2, −1) i przecinającej ujemne
półosie układu współrzędnych w takich punktach, których suma odległości od początku
układu współrzędnych jest najmniejsza.
Coś zrobiłem źle, ale nie wiem gdzie popełniłem błąd. Gdyby ktoś mógł mi go wskazać byłbym
wdzięczny.
A = (−2, −1)
B = (x, 0)
C = (0, b)
D = (0, 0)
Suma odległości punktów B i C od początku układu współrzędnych:
S = x + b
1. Uzależniam b od a:
−1 = −2a + b ⇒ b = 2a − 1
C = (0, 2a − 1)
S = x + 2a − 1
2. Uzależniam x od a:
ax + 2a − 1 = 0
ax = −2a + 1
| −2a + 1 | ||
x = | , gdzie a ∊ (−∞, 0), bo rozpatrywana prosta y = ax + b jest malejąca | |
| a |
| −2a + 1 | 2a2 − 3a + 1 | |||
S(a) = | + 2a − 1 = | , gdzie a ∊ (−∞, 0) | ||
| a | a |
| (4a − 3)a − (2a2 − 3a + 1) | 2a2 − 1 | |||
S'(a) = | = | |||
| a2 | a2 |
| 1 | 1 | |||
a = − | ∨ a = | |||
| √2 | √2 |
| 1 | ||
Smin dla a = | co jest sprzeczne z założeniem, że a ∊ (−∞, 0) | |
| √2 |
