Trapez prostokątny o podstawach a i 2a Mmmmm: Trapez prostokątny o podstawach długości a i 2a oraz krótszym ramieniu równym a podzielono odcinkiem równoległym do podstaw ma dwa trapezy podobne. Uzasadnij że pola tych trapezów są równe a²/2 i a² Jak się zabrać do tego? Rozumiem że w środku tego trapezu jest kwadrat, ale czy to coś pomaga?

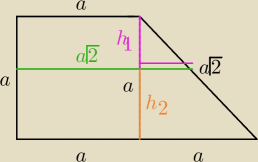
a7: trapezy są podobne czyli

2a		x
	=		⇒ x=a√2
x		a

h=a√2−a=a(√2−1)

	(aP{2}+a)*(a√2−a)		a2
P1=		=
	2		2

	(3a2)		a2
P2=P−P1=		−		=a2
	2		2

c.n.u.

a7: tam oczywiście h=h₁ , a w obliczaniu P₁ powinno być a√2 zamiast aP{2}, P to pole całego trapezu x to zielony odcinek dzielący trapez na trapezy podobne

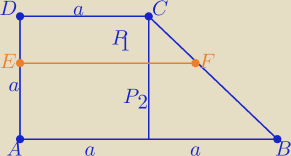
Eta: Można też tak : Z treści zadania : |EF|=√2a*a= a√2 −− średnia geometryczna długości podstaw

	2a
to skala podobieństwa k=		= √2
	a√2

	P2
więc		=k2=2 ⇒ P2=2P1
	P1

P=P₂+P₁ ⇒ P=3P₁

	a+2a		3a2
P=		*a=
	2		2

	a2
to P1=		i P2= a2
	2

===================== i po ptokach