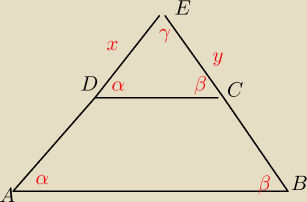
 Podstawy trapezu mają długości 18 i 39, a ramiona 13 i 20. Oblicz pole tego trapezu.
Podstawy trapezu mają długości 18 i 39, a ramiona 13 i 20. Oblicz pole tego trapezu.
| x | 18 | ||
= | |||
| 13+x | 39 |
| 78 | ||
x= | ||
| 7 |
| y | 18 | ||
= | |||
| y+20 | 39 |
| 120 | ||
y= | ||
| 7 |
| 351 | ||
p= | ||
| 7 |
| 351 | 351 | 351 | 78 | 351 | 120 | 3042 | ||||||||
P=√ | ( | −39)( | −13− | )( | −20− | )= | ||||||||
| 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| 324 | ||
p= | ||
| 14 |
| 324 | 324 | 324 | 78 | 324 | 120 | 648 | ||||||||
P=√ | ( | −18)( | − | )( | − | )= | ||||||||
| 14 | 14 | 14 | 7 | 14 | 7 | 7 |
| 3042 | 648 | |||
Ptrapezu= | − | =342 | ||
| 7 | 7 |

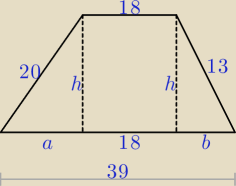 można i tak:
a + b = 39 − 18 = 21 ⇒ b = 21 − a
h2 + a2 = 400
h2 + b2 = 169
−−−−−−−−−−−−−−−
(−) a2 − b2 = 231 ⇒ (a + b)(a − b) = 231 ⇒ 21(a − b) = 231 ⇒ a − b = 11
a − 21 + a = 11 ⇒ a = 16 i h2 + 256 = 400 ⇒ h = ...
można i tak:
a + b = 39 − 18 = 21 ⇒ b = 21 − a
h2 + a2 = 400
h2 + b2 = 169
−−−−−−−−−−−−−−−
(−) a2 − b2 = 231 ⇒ (a + b)(a − b) = 231 ⇒ 21(a − b) = 231 ⇒ a − b = 11
a − 21 + a = 11 ⇒ a = 16 i h2 + 256 = 400 ⇒ h = ...

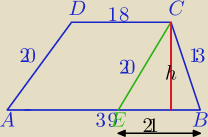 salmandra, krócej i bardziej przyjazne rachunki:
salmandra, krócej i bardziej przyjazne rachunki:
| 21+13+20 | ||
p= | =27 | |
| 2 |
| 1 | ||
PΔEBC= | *21*h=126 | |
| 2 |
