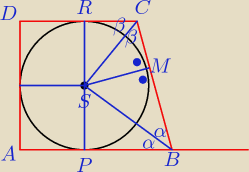trapez! Pati :): Środek okręgu wpisanego w trapez prostokątny znajduje się w odległosiach 4 i 8 od wierzchołków ramienia, które nie jest prostopadłe do podstaw. Sporzadz rysunek, wprowadz oznaczenia i oblicz pole trapezu. Proszę o pomoc!

Basia: SC = 4 SB = 8 trapez jest opisany na okręgu ⇒ AB+CD = AD+BC 2α+2β+90+90=360 2(α+β)=180 α+β=90 β=90−α

	SP		r
sinα=		=
	SB		8

	RS		r
sinβ=		=
	SC		4

sinα=¹₂sinβ=¹₂*sin(90−α) = ¹₂*cosα cosα=2sinα sin²α+cos²α=1 sin²α+4sin²α=1 5sin²α=1 sin²α=¹₅

	1
sinα=
	√5

	2
cosα=
	√5

r		2
	=
4		√5

	8		8√5
r=		=
	√5		5

	16		16√5
|AD|=2r =		=
	√5		5

	PB
cosα=
	SB

	2		16		16√5
PB = SB*cosα=8*		=		=
	√5		√5		5

	24√5
AB=AP+PB = r+PB =
	5

	16√5
BM=BP=
	5

	CM
cosβ=
	SC

cosβ=sinα

1		CM
	=
√5		4

	4		4√5
CM =		=
	√5		5

	20√5
[N[BC=BM+MC=
	5

	4√5
RC=MC=
	5

	12√5
CD=RD+RC=r+RC=
	5

podstaw do wzoru na pole

Bogdan: Proponuję takie rozwiązanie: x + y = √4² + 8² = √80 = 4√5

(x + y)*r		4*8		4*8		8
	=		⇒ r =		=
2		2		4√5		√5

Pole trapezu

	1		1		64		8
P = 2r2+2*		*r*x+2*		*r*y = 2r2 + r(x + y) = 2*		+		*4√5 = ...
	2		2		5		√5