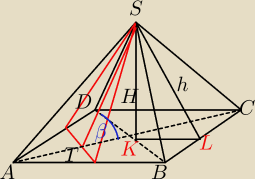
Mógłby ktoś zerknąć i sprawdzić czy dobrze? FUITP: W ostrosłupie prawidłowym czworokątnym kąt ściany bocznej przy wierzchołku ostrosłupa ma miarę α. Oblicz tangens kąta, jaki tworzy z płaszczyzną podstawy płaszczyzna przechodząca przez wierzchołek ostrosłupa oraz środki dwóch sąsiednich boków podstawy.

	H
tgβ =
	|TK|

|AB| = a

	a√2
|AC| = a√2 ⇒ |TK| =
	4

	α		a		a
tg		=		⇒ h =
	2		h		α   2tg   2

	1		a√1−tg2α2
H2 = h2 −		a2 ⇒ H =
	4		2

	a√1−tg2α2		4		2√1−tg2α2
tgβ =		*		=		= √2−2tg2α2
	2		a√2		√2

f123: tak

f123: jest tylko jeden blad w zapisie

	α		a
tg		=		, ale h wyznaczone masz juz dobrze z ta '2' ktorej wczesniej nie napisales
	2		2h

FUITP: Racja, źle przepisałem. Dzięki!