Dany jest trójkąt prostokątny abc Filip: Dany jest trójkąt prostokątny ABC o przyprostokątnych długości lABl = 4 i lBCl= 2. Odcinek PQ dzieli ten trójkąt na dwie figury o równych polach. Oblicz obwód trójkąta APQ. Zaloguj cyfrę jedności i dwie pierwsze cyfry po przecinku otrzymanego wyniku. Jak zabrać się do tego zadania? Kompletnie nie mam pojęcia.

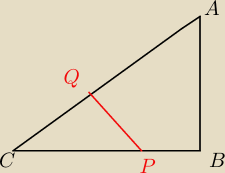
salamandra: Na pewno taki jest rysunek podany, czy ty go narysowałeś?

Filip: Taki jest rysunek podany w książce. Przy Q i B jest kat prosty

Filip: Tzn na dole jest A P B. Wierzchołek C jest na gorze

Gangster: Narysuj dokladnie ten rysunek wraz z oznaczeniami.

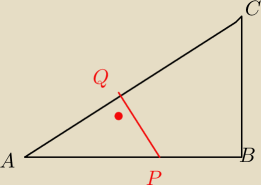
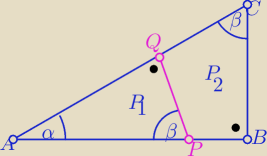
salamandra: tak?

Gangster: Obliczenia do rysunku salamandry: P ABC = 4 ABC podobny do QPC k=2 ⇒QC=1 P PQC=1 ⇒ PQ=2 AQ= √20 −1 teraz policz Pole trojkata prostokatnego APQ

a7: mi już chyba wyszło, zaraz napiszę

Gangster: Obliczenia do rysunku który salamandra wrzucił jako pierwszy

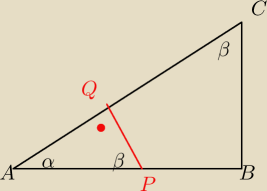
salamandra: AB=4 BC=2 AC=√20 Pabc=4 Papq=2 k=√2

	√20		√40
AQ=		=		=√10
	√2		2

	2
QP=		=√2
	√2

	4
AP=		=2√2
	√2

Ob=√10+√2+2√2=3√2+√10

salamandra: sory, źle wyznaczyłem

	4
AQ=		=2√2
	√2

QP=√2 AP=√10 Obwód ten sam

Filip: Dziękuję bardzo

Gangster: fakt, uciekl mi kwadrat przy skali, zamysł dobry ale blad dalej w obliczeniach.

salamandra: Nie daję gwarancji, że jest to dobrze, masz odpowiedź tego rozwinięcia dziesietnego?

f123: Mi wyszlo 3√2 + √10

Filip: Salamandra wyszło dobrze. Wynik taki jest w odpowiedziach a liczby do zakodowania do 740 więc wszystko wychodzi elegancko dzięki

salamandra: to git

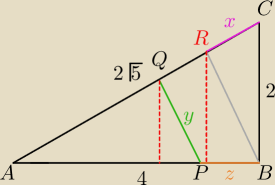
a7: P_ABC=4 P/2=2 h=4√5/5 (BR) z podobieństwa trójkątów ABC i BRC x=2√5{5} P₁=P₂ 1/2*4|PR|=4−1/2*2√5/5*4√5/5 czyli PR=8/5

	2		85
z podobieństwa trójkątów ABC i ARP		=		czyli PB=z=16/5=315
	4		z

2√58|PQ|=2*16/5 czyli |PQ|=y=16/25√5

	80+48√5
czyli OBWÓDΔAPQ=315+16/25√5+32/25√5=		≈7,49325≈7,49
	25

a7: a więc u mnie błędy i źle....

Karol: Wiem, ze zadanie ma pewnie kilka lat, ale pytanie. Skad wiadomo, ze ABC jest podobny do QPC i ze k = 2? Nie jest dany ani jeden bok QPC, wiec skad wynika wartość k?

fil: Z cechy (kk) ΔAPQ∼ΔABC P_ABC=P= 4 to P₁=2

P1		1		√2
	= k2 ⇒ k2=		to k=
P		2		2

|AC|= √20= 2√5 to obwód ABC L= 6+2√5

	√2
więc obwód APQ L1= k*L =		(6+2√5)
	2

L₁= 3√2+√10 ===========