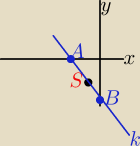
geo mr t: Prosta k o równaniu y=ax + b, gdzie a<0, przechodząca przez punkt S=(−3, −4), odcina na ujemnych półosiach układu współrzędnych odcinki, których suma długości jest najmniejsza z możliwych. Wyznacz równanie prostej k oraz tę najmniejszą sumę długości odcinków. S(−3;−4) A(x,0) B(0;y)

Bleee: Wyznacz 'y' w zależności od 'x'. Szukasz minimum z |x| + |y|

Layla: 1. Podstaw do prostej współrzędne punktu S i wyznacz 'b'. 2. Do równanie podstaw 'b' z 1. i wylicz 'x' uzależnione od parametru 'a'. 3. Długości odcinków to 'x' i 'b'. Sumujesz je. 4. Liczysz pochodną funkcji sumy odcinków. Jej miejsca zerowe, szukasz ekstremów. 5. Wyznaczasz równanie prostej. 6. Liczysz długości odcinków.

mr t:

	4+y−3a
Nie wiem jak wyznaczyć y w zależności od x... dochodzę do momentu gdy x=
	a

Jerzy: Nie wiem, czy dobrze to policzyłeś, ale: ax = 4 + y − 3a ⇔ y = ax + 3a − 4

f123: y = ax + 3a − 4 wspolrzedne punktu B (0, 3a − 4) wspolrzedne punkt A: Srpawdzasz, dla jakiego 'x' f(x) = 0 czyli 0 = ax + 3a − 4

	4 − 3a
x =
	a

wredulus_pospolitus: y=ax+b −4 = −3a + b −−−> b = 3a − 4 więc mamy równanie: y = ax + 3a − 4 stąd mamy współrzędne punktów:

	4−3a
(0, 3a−4) oraz (		; 0)
	a

wartość bezwzględną nakładasz (w końcu a<0) sumujesz ... i otrzymujesz funkcję ze zmienną 'a' ... pochodna ... szukasz minimum

mr t: okej, dziękuje wszystkim, zrozumiałem