proste na płąszczyźnie Matfiz: Dwie proste równoległe AB i CD odległe od siebie o 6cm leża na płaszczyźnie π . punkt S leży poza tą płaszczyzną w odległości 25cm od prostej AB i 29cm od prostej CD. wyznacz odległość punktu S od płaszczyzny π. mógłby mi ktoś wytłumaczyć jak to ogarnąć?

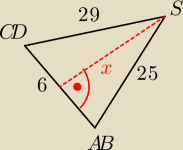
wredulus_pospolitus: wyznacz 'x'

Matfiz: Jedno pytanie − dlaczego trójkąt?

Matfiz: i gdzie tutaj są proste AB i CD? Chyba czegoś nie rozumiem kurcze

wredulus_pospolitus: Ułóż dwa sznurki na stole (równolegle) −−− to Twoje proste. Nad stołem trzymaj piłeczkę (punkt S). Jaki odcinek będzie odległością punktu S od prostej AB (jeden ze sznurków), a jaki będzie odcinek dla prostej CD A jaki odcinek będzie odległością tej piłeczki od stołu?

Matfiz: Aaaaaaa dobra dziękuję ci bardzo za wytłumaczenie, cały czas źle interpretowałem zadanie ostatnie pytanie − odległość punktu S od prostej AB i CD wcale nie oznacza że odcinek od punktu S do prostej AB albo CD musi padać pod kątem prostym?

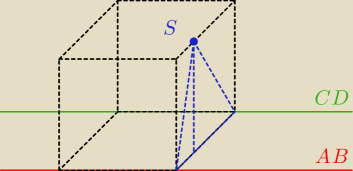
wredulus_pospolitus: to co wcześniej narysowałem to ten niebieski trójkąt

wredulus_pospolitus: odległość punktu S od prostej AB oznacza, że tenże odcinek (będący 'odległością' ) jest PROSTOPADŁY do prostej ... patrz rysunek z 23:32

wredulus_pospolitus: 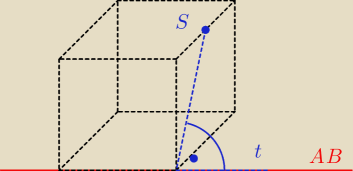taki kąt prosty <−−− dlatego ten odcinek będzie odległością punktu S od prostej AB,

Matfiz: Hmmm czyli jednocześnie prosta z punktu S do prostej AB i prosta z punktu S do prostej CD pada pod kątem prostym ?

Matfiz: Już dużo się rozjaśniło, dziękuję za pomoc nigdy bym na to nie wpadł serio

wredulus_pospolitus: Tak jak mówiłem na początku ... stań nad stołem (nie nad jego krawędzią) i palcem 'podążaj' po prostej do krawędzi tegoż stołu. Kiedy Twój palec będzie wytyczał odległość Twoich oczu od krawędzi stołu? Kiedy Twój palec będzie ... 'prostopadły' do krawędzi stołu. I teraz jeżeli zaczniesz (nie zmieniając pozycji) prowadzić palec do drugiej (przeciwnej) krawędzi stołu ... to sytuacja się powtórzy −−− a odległość od stołu to będzie 'paluch spuszczony w dół' czyli nic innego jak wysokość tegoż trójkąta.

Matfiz: dziękuję za wytłumaczenie, nie miałem takich rzeczy w szkole niestety a do matury może się przydać bo jest za miesiąc

wredulus_pospolitus: Wątpię by takie zadanie było na maturze (chociaż arkuszy nie jestem korepetytorem, więc nie wiem jaki dokładnie jest zakres) −−− geometria przestrzenna raczej się sprowadza do zadań na bryłach przestrzennych (walce, stożek, ostrosłup, graniastosłup, kula). To zadanie bardziej by pasowało na 1−2 rok studiów technicznych (na niektórych kierunkach).

Matfiz: też mi się tak wydaje powiem ci szczerze dlatego skupiłem się bardziej na ostrosłupach i graniastosłupach ze stereometrii ale byłem strasznie ciekaw jak zrobić to zadanie

wredulus_pospolitus: No to teraz wiesz

wredulus_pospolitus: A jak pójdziesz na studia na jakiś kierunek gdzie będzie "kreska", to i rzutów się nauczysz i będziesz wiedział/widział jak powstał rysunek z 23:19

wredulus_pospolitus: "kreskę" *

Matfiz: najpierw się trzeba na studia dostać

Mila: Najlepiej oblicz pole Δ z wzoru Herona, a potem z innego wzoru oblicz wysokość. Jeśli zaczniesz z Pitagorasem, to będzie niespodzianka.

wredulus_pospolitus: Miluś −−− jeżeli wcześniej sprawdzi czy to jest ostrokątny czy rozwartokątny, to niespodzianki nie będzie. Ale masz rację −−− ja pierwsze co to także myślałem o wzorze Herona

Mila: Pozdrawiam.

Matfiz: Racja, Pitagorasem ciężko może być dzięki za pomoc