planimetria f123: Punkt D jest punktem stycznosci okregu wpisanego w trojkat ABC z bokiem BC. WYznacz pole trojkata ABC wiedzac, ze kat BAC = α i |BD| = m oraz |CD| = n

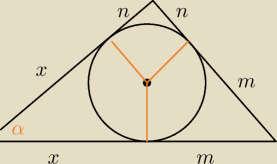
wredulus_pospolitus: 'mocno na chama' z tw. cosinusów: (n+m)² = (x+m)² + (x+n)² − 2(x+m)(x+n)cosα −−− wyznaczamy 'x' do wzoru Herona. Jednak obliczenia będą TRAGICZNE.

f123: na chama taka metoda to z saizou robilem, zrezygnowalismy po tw cosinusow

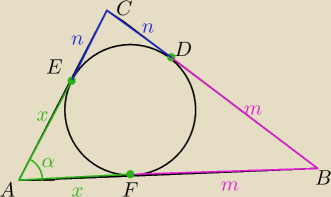
a7: z tw. cosinusów (n+m)²=(n+x)²+(m+x)²−2*(n+x)(m+x)cosα wyliczamy x (wychodzi nieładne) P_ΔABC=1/2(n+x)(m+x)sinα

a7: a jest odpowiedź?

f123: jest.

f123:

	mn
P =
	α   tg   2

wredulus_pospolitus: faktycznie ... z tego wzoru na pole można skorzystać ale tak jak pisałem wcześniej −−− postać samego 'x' do najpiękniejszych nie będzie wyglądać

f123: @wredulus czemu na discorda juz nie wchodzisz?

wredulus_pospolitus: bo mam trochę roboty i nie mam czasu

f123: Nie dziwie sie, twoja praca szczegolnie wymaga czasu, wracaj jak najszybciej bedziesz mogl

wredulus_pospolitus: dostałem spore zlecenie na przeliczenie budynków −−− trochę roboty będę miał z tym. Co do samego zadania −−−− powyższy wzór widziałem tylko przy szczególnym przypadku czyli przy trójkącie prostokątnym (wtedy tg(α/2) = 1 ... więc P_ABC = n*m), ale na dobrą sprawę to nie wiem w jaki sposób wyprowadzić tą ogólną postać. Eta bądź Mila mogą wiedzieć.

f123: Probowalem jedynie promien okregu wpisanego w ten trojkat uzaleznic od kata alfa, m i n, oraz wlasnie ten niewiadomy odcinek, ale kosmiczne liczby wychodza, i finalnie pole, bardzo odlegle od wyniku

a7: dobra, chyba mam już piszę

wredulus_pospolitus: no dobra ze wzoru Herona: P = √p(p−a)(p−b)(p−c) = √(x+n+m)*x*n*m

	2P
r =		−> P = r*(x+y+z)
	2(x+y+z)

	√x*n*m
stąd wiemy, że r =
	√x+y+z

tak więc: P*r = x*m*n

	x*m*n
P =
	r

	m*n
P =
	r   x

	m*n
P =
	tg(α/2)

wyprowadzone ... ale gdybym nie wiedział 'czego szukać' to bym raczej tą drogą nie szedł.

wredulus_pospolitus: @a7 −−− no to Ciebie ubiegłem Wybacz.

f123: Oznaczenia x, y z, duzo mowia

a7: P=1/2(n+x)(m+x)*sinα=1/2(nm+mx+nx+x²)sinα z tw. cosinusów

	2nm
(x2+nx+mx+nm)=
	1−cosα

	nm*sinα		nm
P=		=
	1−cosα		tg(α/2)

f123: a skad sie wzirelo ostatnie przekstzalcenie?

wredulus_pospolitus: oj ... miało być x + n + m odruchowo pisałem x,y,z

wredulus_pospolitus: stąd:

sina		2sin(a/2)cos(a/2)		cos(a/2)
	=		=
1 − cosa		1 − (1 − 2sin2(a/2))		sin(a/2)

f123: Cos namieszales, albo to ja nic nie rozumiem

a7: sinα=2sin(α/2)cos(α/2) 1−cosα=1−1+2sin²(α/2)

	sin(α/2)		1
wychodzi		=
	cos(α/2)		tg(α/2)

f123: Wzor herona − ok, co w nastepnej linijcie sie dzieje?

wredulus_pospolitus:

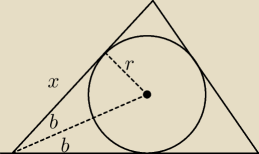
	a+b+c		2(x+n+m)
p =		=		= (x+n+m)
	2		2

ze wzoru Herona: P = √(x+n+m)*x*n*m ze wzoru na 'r' okręgu wpisanego w trójkąt:

	2P		P		√(x+n+m)*x*n*m		√x*n*m
r =		=		=		=
	a+b+c		x+n+m		x+n+m		√x+n+m

P = √(x+n+m)*x*n*m //*r P*r = r*√(x+n+m)*x*n*m

	√x*n*m
P*r =		*√(x+n+m)*x*n*m = x*n*m
	√x+n+m

	x*n*m		n*m		r
P =		=		natomiast		= tg(b) = tg(α/2) (patrz rysunek)
	r		r   x		x

f123: Czeka mnie filologia polska w Poznaniu. Wszystko jasne.

wredulus_pospolitus: W Poznaniu Uuuuuu ... wysoko postawiona poprzeczka

f123: wlasnie pisze 3 rozprawki na jutro. Dzisiaj tez dowiedzialem sie ciekawej rzeczy − ze liczba "−2" takze jest parzysta

wredulus_pospolitus: noooo ... tak ... a czemu by nie miała być parzysta Parzysta to w końcu każda liczba CAŁKOWITA (a nie naturalna), która przy dzieleniu przez 2 daje resztę 0.

f123: Zalozylem ze zadna ujemna nie jest, i po 10 razie "submitowania" (10x testy przeszly na czerwono) poszedlem sie upewnic, ale w koncu oddalem ZOPTYMALIZOWANE rozwiazanie

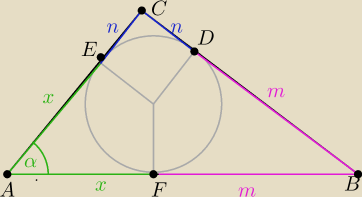
a7: jeszcze ode mnie wersja "dla potomnych" P_ΔABC=1/2((n+x)(m+x)sinα=1/2(nm+mx+nx+x²)sinα z tw. cosinusów (n+m)²=(n+x)²+(m+x)²−2(m+x)(n+x)cosα 2x²+2nx+2mx+2nm−4nm−2cosα(nm+nx+mx+x²)=0 (x²+nx+mx+nm)(1−cosα)=2nm

	2nm
(x2+nx+mx+nm)=
	1−cosα

więc

	1		2nm
PΔABC=1/2*(nm+mx+nx+x2)*sinα=		*		*sinα=
	2		(1−cosα)

	nm*2sin(α/2)cos(α/2)
		=
	1−1+2sin2(α/2)

	nm
=
	tgα2

====

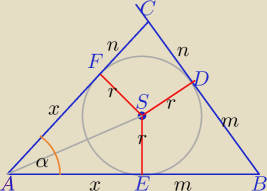
Mila: P− pole ΔABC

	x		α
1) W ΔAES:		=ctg
	r		2

2) Heron i P=p*r p=x+m+n P²=(x+m+n)x*m*n P=(x+m+n)*r −−−−−−−−−−−− dzielę stronami

	(x+m+n)x*m*n		x*mn
P=		⇔P=		⇔
	(x+m+n)*r		r

	α
P=mn*ctg
	2

===============