dowodzenie nierówności jaros: x⁴ − 6x³ + 11x² − 6x + 1 ≥ 0 Umie ktoś to rozwiązać Hornerem bo ja nie mam na to innego pomysłu

salamandra: jaka jest treść zadnaia?

jaros: Wykaż, że dla każdej liczby rzeczywistej x prawdziwa jest nierówność x(x − 1)(x − 2)(x − 3) + 1 ≥ 0

Gangster: Moze pochodna i monotonicznosc?

ABC: zauważ że x(x−3)=x²−3x (x−1)(x−2)=x²−3x+2 zatem podstaw t=x²−3x+1 już widzisz?

f123: (x² − 3x)(x² − 3x + 2) + 1 >= 0 (x² − 3x)(x² − 3x + 1) + x² − 3x + 1 >= 0 (x² − 3x + 1)² >= 0

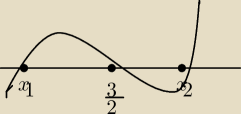
salamandra: Za pomocą pochodnej (oczywiście to niejedyny sposób) f'(x)=4x³−18x²+22x−6 f'(x)=0 ⇔ 4x³−18x²+22x−6=0

	3
W(		)=0
	2

3
	jest pierwiastkiem wielomianu 4x3−18x2+22x−6
2

	3
(4x3−18x2+22x−6):(x−		)=4x2−12x+4
	2

4x²−12x+4=0 Δ=144−64=80 √Δ=4√5

	12−4√5		3−√5
x1=		=		(√5 > 2 i < 3), więc x1 > 0
	8		2

	3+√5
x2=
	2

	3−√5		3+√5
min dla x=		oraz x=
	2		2

	3
max dla x=
	2

lim (x⁴−6x³+11x²−6x+1)= +∞ x−>+∞ lim(x⁴−6x³+11x²−6x+1)=+∞ x−>−∞

salamandra: oczywiście jeszcze powinieneś sprawdzić te wartości które wyliczyłem, czyli f(x1) i f(x2) czy są ≥ 0

jaros: @salamndra dziękuję za policzenie z rachunku różniczkowego, @f123 Co się zadziało między 2 a 3 linijką? wiem, że wyłączyłeś 1 ale jak?

jaros: @salamadnra tak samo bym zrobił to z rachunku różniczkowego

f123: (x² − 3x)(x² − 3x + 2) + 1 = (x² − 3x)(x² − 3x + 1 + 1) = (x² − 3x)(x² − 3x + 1) + (x² − 3x)

jaros: Dla min i max = 0 oraz funkcja w nieskończonościach przyjmuje wartości nie ujemne zatem ckd.

ABC: gdybyś podstawił jak ci radziłem dostałbyś (t−1)(t+1)+1≥0 , czyli t²≥0 i byś wiedział skąd

jaros: @ABC no tak wsm to teraz dużo bardziej widoczne i wystarczy tylko napisać, że kwadrat liczby zawsze jest nie ujemy i wystarczy?

jaros: @f123 czyli wyciąganie "1" z iloczynu 2 wyrażeń to tak jakby przepisać wyrażenie, które nie przekształcamy?

ABC: tak, wystarczy napisać że kwadrat jest nieumny

Repo: No właśnie mógłby mi ktoś rozpisać zapis @f123 ? Skąd z "1" wziął się nawias (x²−3x) godz. 14:07

f123: @Repo a pojdz od tylu, mamy wyrazenie (x² − 3x)(x² − 3x + 1) + (x² − 3x). Wyciagami wspolny czynnik przed nawias − w tym przyadku (x² − 3x). W nawiasie dostanimy: (x² − 3x)(x² − 3x + 1 + 1)

Mariusz: x⁴ − 6x³ + 11x² − 6x + 1 √1 − 6x + 11x² − 6x³ + x⁴≈1−3x+x² 1 0−6x+11x² |(2−3x)(−3x) −6x+9x² 0x+2x²−6x³+x⁴|(2−6x+x²)(x²) 2x²−6x³+x⁴ 0x² +0+x³+0x⁴ zatem (1−3x+x²)²=1 − 6x + 11x² − 6x³ + x⁴ Sposób wzięty z pisemnego sposobu obliczania pierwiastków