
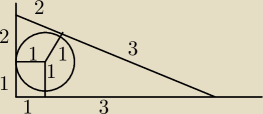
 podany trójkąt nie może być prostokątny gdyż musiałby mieć wszystkie boki będące liczbami
całkowitymi(3,4,5)
to wtedy trzecia wysokość nie byłaby liczbą całkowitą
?
podany trójkąt nie może być prostokątny gdyż musiałby mieć wszystkie boki będące liczbami
całkowitymi(3,4,5)
to wtedy trzecia wysokość nie byłaby liczbą całkowitą
?
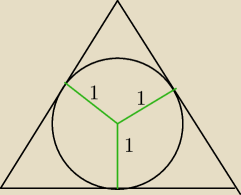 hmin>2r i h jest calkowite czyli hmin=3
gdyby h było równe 4, 5, 6 czy więcej np w trójkącie równoramiennym to pozostałe wysokości
byłyby mniejsze niż 3, a więc nie byłyby liczbami całkowitymi
podobnie w każdym innym trójkącie ostrokątnym przynajmniej jedna wysokość byłaby mniejsza niż
trzy, a więc nie całkowita
jeśli chodzi o trójkąt rozwartokątny to wysokość z wierzchołka kąta rozwartego nie spełniałaby
warunków zadania, a więc warunki zadania spełnia tylko trójkąt równoboczny
c.n.w.
?
hmin>2r i h jest calkowite czyli hmin=3
gdyby h było równe 4, 5, 6 czy więcej np w trójkącie równoramiennym to pozostałe wysokości
byłyby mniejsze niż 3, a więc nie byłyby liczbami całkowitymi
podobnie w każdym innym trójkącie ostrokątnym przynajmniej jedna wysokość byłaby mniejsza niż
trzy, a więc nie całkowita
jeśli chodzi o trójkąt rozwartokątny to wysokość z wierzchołka kąta rozwartego nie spełniałaby
warunków zadania, a więc warunki zadania spełnia tylko trójkąt równoboczny
c.n.w.
?
| 1 | 1 | 1 | 1 | ||||
+ | + | = | |||||
| ha | hb | hc | r |
| 1 | 1 | 1 | ||||
+ | + | =1 | ||||
| ha | hb | hc |
| 1 | 1 | 1 | ||||
to ha=hc=hb=3 bo ( | + | + | =1 | |||
| 3 | 3 | 3 |