pole hania: Dane są kolejne długości boków czworokąta a,b,c,d. Wykaż że

	(a+c)(b+d)
P≤
	4

ford:

(a+c)(b+d)		a*b + a*d + b*c + c*d
	=
4		4

	1		1
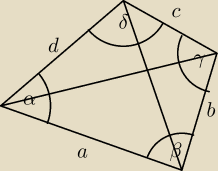
P =		*a*d*sinα +		*b*c*sinγ
	2		2

	1		1
P =		*a*b*sinβ +		*c*d*sinδ
	2		2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	1		1		1		1
2P =		*a*d*sinα +		*b*c*sinγ +		*a*b*sinβ +		*c*d*sinδ
	2		2		2		2

	a*d*sinα + b*c*sinγ + a*b*sinβ + c*d*sinδ
P =
	4

sinα ≤ 1 → a*d*sinα ≤ a*d sinβ ≤ 1 → a*b*sinβ ≤ a*b sinγ ≤ 1 → b*c*sinγ ≤ b*c sinδ ≤ 1 → c*d*sinδ ≤ c*d −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− a*d*sinα + b*c*sinγ + a*b*sinβ + c*d*sinδ ≤ a*d + b*c + a*b + c*d

a*d*sinα + b*c*sinγ + a*b*sinβ + c*d*sinδ		a*d + b*c + a*b + c*d
	≤
4		4

	a*d + b*c + a*b + c*d
P ≤
	4