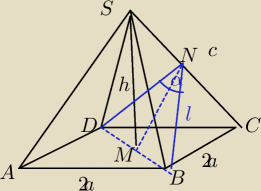
stereometria salamandra: W ostrosłupie prawidłowym czworokątnym ABCDS o podstawie ABCD wysokość jest równa h , a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę α . Oblicz objętość tego ostrosłupa.

	a√2
l=
	α   sin   2

mogę prosić o jakąś podpowiedź jak teraz "a" uzależnić od h lub od kąta?

Eta:

	a√2
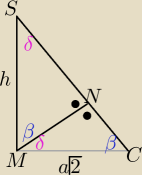
1/ |BM|=a√2 tg(α/2) = |MB|/ |MN| ⇒ |MN|=
	tg(α/2)

2/ z tw. Pitagorasa w ΔMCN |NC|=..........

	a√2√tg2(α/2)−1
|NC|=		.
	tg(α/2)

3/ z podobieństwa trójkątów MNC i MNS

h		|MN|
	=		⇒ 4a2= ............=Pp
a√2		|NC|

V= ............

Eta: I co?

salamandra: Nie rozumiem dlaczego w trójkącie MCS przy "N" jest kąt prosty, skoro to krawędź NB=l tworzy kąt prosty z krawędzią SC

Mila: SC jest prostopadła do płaszczyzny DBN to jest prostopadła do każdej prostej leżącej w pl.DBN i przechodzącej przez punkt przebicja N. ⇔SC⊥MN

Eta:

salamandra: 2) NC²+MN²=MC²

	a√2
NC=a√2−
	α   tg   2

	α   a√2*tg( )−a√2   2		α   a√2(tg −1)   2
NC=		=
	α   tg   2		α   tg   2

Dlaczego u Ciebie jest tg² w liczniku oraz ten pierwiastek?

salamandra: nie było pytania− cd..

h		a√2		a√2√tg2α2−1
	=		:
a√2		tgα2		{tgα2}

mnożę na krzyż, nie mogłem tylu ułamków pod jednym zapisać, ale zamysł jest tak jak u Ety w 3)

	a√2		2a2
1) a√2*		=
	α   tg   2		α   tg   2

	α   a√2*√tg2 −1   2
2) h*
	α   tg   2

2a2		α   a√2*√tg2 −1   2
	=h*		<− jest to równe wtedy i tylko wtedy,
α   tg   2		α   tg   2

gdy liczniki są równe

	α
2a2=h*a√2*√tg2		−1
	2

2a2		α
	=h*√tg2		−1
a√2		2

2√2a2		α
	=h*√tg2		−1
2a		2

	α
a√2=h*√tg2		−1
	2

	α
2a=h√2*√tg2		−1
	2

	α		α
Pp=(h√2*√tg2		−1)2=2h2*(tg2		−1)
	2		2

	1		α		2		α
V=		*2h2*(tg2		−1)*h=		h3(tg2		−1)
	3		2		3		2

jest ok?

f123:

	−4h3cosα
Wynik ok, po przeksztalceniach dostajemy V =
	3 + 3cosα

salamandra: dzięki wariat

f123: oczywiscie wiadomo, ze kat α ∊ (90, 180), dlatego mamy '−' w wyniku

salamandra: fil wbij na discord