geometria analityczna
salamandra:
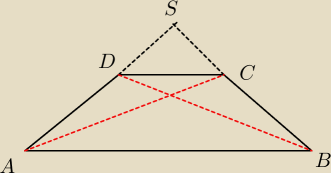
Przedłużenia ramion AD i BC trapezu równoramiennego ABCD przecinają się w punkcie S = (−
14,15) . Wyznacz współrzędne wierzchołków B i D tego trapezu, jeżeli A = (− 8,− 15) i C =
(− 9,14) .
A=(−8,−15)
C=(−9,14)
S=(−14,15)
1) |CS|
2=(−14+9)
2+(15−14)
2=26
|CS|=
√26
|AC|
2=(−9+8)
2+(−15−14)
2=842
|AC|=
√842
2)prosta AS:
−15=−8a+b
15=−14a+b
15=8a−b
15=−14a+b
30=−6a
a=−5
b=−55
y=−5x−55
3) D=(x,−5x−55)
|SD|
2=26
26=(x+14)
2+(−5x−55−15)
2=x
2+28x+196+25x
2+700x+4900=26x
2+728x+5096
26x
2+728x+5096−26=0
26x
2+728x+5070=0
x
2+28x+195=0
Δ=784−780=4
x1=−15
x2=−13
D
1=(−15,20) <− odrzucam
D2=(−13,10)
4) prosta CS:
14=−9a+b
15=−14a+b
−14=9a−b
15=−14a+b
5) |BD|
2=842
D=(−13,10)
| | 1 | | 61 | | 1 | | 22 | |
842=(x+13)2+(10+ |
| x− |
| )2=x2+26x+169+ |
| x2− |
| x+U}{ |
| | 5 | | 5 | | 25 | | 25 | |
| | 26 | | 628 | | 4346 | |
121}{25}= |
| x2+ |
| x+ |
| |
| | 25 | | 25 | | 25 | |
| 26 | | 628 | | 4346 | |
| x2+ |
| x+ |
| −842=0 |
| 25 | | 25 | | 25 | |
| 26 | | 628 | | 16704 | |
| x2+ |
| x− |
| =0 / * 25 |
| 25 | | 25 | | 25 | |
26x
2+628x−16704=0
13x
2+314x−8352=0
Δ=532900
√Δ=730
x2=16
B=(16,9)
D=(−13,10)
Jest ok? Jeśli tak, to jeszcze mam pytanie jakie uzasadnienie należy napisać, gdy odrzucam
którąś ze współrzędnych − dla mnie jest to widoczne, ale jak to należy skomentować?
2 maj 12:09
wredulus_pospolitus:
Chyba czegoś zapomniałeś dodać w treści zadania.
Masz podane tylko trzy punkty (wierzchołki trójkąta równoramiennego)

2 maj 12:24
salamandra: Podałem całą treść
2 maj 12:27
Eta:
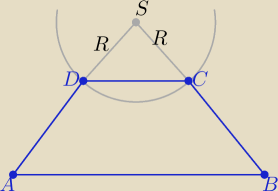
→
SC=[−5,−1]
R
2= |SC|
2=26
| | 1 | | 1 | |
aSC= |
| prosta SC: y= |
| (x+14)+15 |
| | 5 | | 5 | |
o:(S,R) : (x+14)
2+(y−15)
2=26
Rozwiązując układ równań o kręgi i prostej SC otrzymasz
współrzędne punktu D
| | 1 | |
(x+14)2+( |
| (x+14)2=26 /*25 |
| | 5 | |
(x+14)
2=25 ⇒ x= −9 = x
C v x=−19= x
D to y
D= 14
D(, −19,14)
==========
dalej już prosto

dokończ..........
2 maj 13:46
salamandra: Dlaczego rozwiązując ukłąd równań okręgu i prostej SC otrzymam punkt D, skoro one się
przecinają w punkcie C, a nie D?
Poza tym, czy moje rozwiązanie jest złe? Zwykle tak rozwiązywałem tego typu zadania

2 maj 13:54
Eta:
Trapez jest równoramienny więc ten okrąg przecina
i prostą SC i prostą SD ( co masz na rysunku
2 maj 13:58
Eta:
Na Twoje
"rozlazłe" opisy − zabraknie Ci czasu na maturze !

2 maj 13:59
salamandra: Ok, już rozumiem, a moje podejście do zadania było złe, czy gdzieś błąd obliczeniowy
prawdopodobnie zrobiłem?
2 maj 14:00
an:
to obliczyłeś wyżej SC=
√26 SA=
√936 ⇒ otrzymujemy stosunek SA/SC=6
Korzystając z podobieństwa SDC i SAB i że są to trójkąty równoramienne ,
| | xSA | |
xSA=6 ⇒ xSD= |
| =1 : xSC=5 ⇒ xSB=xSC*6=30 |
| | 6 | |
| | ySA | |
ySA=30⇒ ySD= |
| =5 : ySC=1 ⇒ ySB=ySC*6=6 |
| | 6 | |
S=(−14,15) D=(−13,10) B=(16,9)
Mam nadzieję, że rozumiesz p/w. Ile czasu potrzeba na takie rozwiązanie, a ile na te wyżej

2 maj 17:15
salamandra: To w takim razie ja mam dobrze, czy Eta?

Próbowałem coś na początku z podobieństwa, ale, że chodziło o współrzędne punktu, to nie
wiedziałem jak to ugryźć, więc zrobiłem jak umiem
2 maj 17:18
f123: @Eta powinno byc (x + 14)2 = 1
2 maj 17:26
an: Jak napiszę, że Eta namieszała to się obrazi. Już pisałem skorzystaj z Geogebry , a na maturze
z kratkowanego papieru na którym można co najmniej oszacować wyniki zadań.
2 maj 17:31
salamandra: to jeśli Ty się nie obrazisz, to powiem, że nie rozumiem zbytnio Twojego rozwiązania, rozumiem
jedynie pierwszą linijkę, a nie wiem jak wykorzystać podobieństwo do współrzędnych punktów
2 maj 17:34
an:
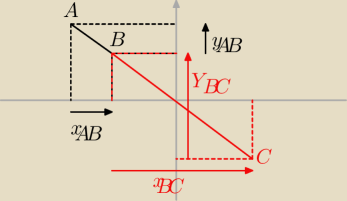
Jeżeli ABC leża na jednej prostej i BC=k*AB
to X
BC=k* x
AB i y
BC=k* y
AB czy to rozumiesz
2 maj 18:00
salamandra: xAB to odległość „x” od A do B?
2 maj 18:44
an:
tak , czyli jest to długość rzutu prostokątnego odcinka AB na oś x to samo dotyczy "y"
2 maj 18:51
salamandra: Teraz rozumiem, dzięki
2 maj 18:55
Eta:
@
an
Nic nie namieszała

( tylko nie mogę znaleźć błędu w rachunkach
Twój sposób rozwiązania jest najkrótszy ! Łap ..........

2 maj 20:58
Mila:
SC→=[5,−1]
2 maj 21:09
Eta:
Dzięki
Mila 
2 maj 21:18
 Przedłużenia ramion AD i BC trapezu równoramiennego ABCD przecinają się w punkcie S = (−
14,15) . Wyznacz współrzędne wierzchołków B i D tego trapezu, jeżeli A = (− 8,− 15) i C =
(− 9,14) .
A=(−8,−15)
C=(−9,14)
S=(−14,15)
1) |CS|2=(−14+9)2+(15−14)2=26
|CS|=√26
|AC|2=(−9+8)2+(−15−14)2=842
|AC|=√842
2)prosta AS:
−15=−8a+b
15=−14a+b
15=8a−b
15=−14a+b
30=−6a
a=−5
b=−55
y=−5x−55
3) D=(x,−5x−55)
|SD|2=26
26=(x+14)2+(−5x−55−15)2=x2+28x+196+25x2+700x+4900=26x2+728x+5096
26x2+728x+5096−26=0
26x2+728x+5070=0
x2+28x+195=0
Δ=784−780=4
x1=−15
x2=−13
D1=(−15,20) <− odrzucam
D2=(−13,10)
4) prosta CS:
14=−9a+b
15=−14a+b
−14=9a−b
15=−14a+b
Przedłużenia ramion AD i BC trapezu równoramiennego ABCD przecinają się w punkcie S = (−
14,15) . Wyznacz współrzędne wierzchołków B i D tego trapezu, jeżeli A = (− 8,− 15) i C =
(− 9,14) .
A=(−8,−15)
C=(−9,14)
S=(−14,15)
1) |CS|2=(−14+9)2+(15−14)2=26
|CS|=√26
|AC|2=(−9+8)2+(−15−14)2=842
|AC|=√842
2)prosta AS:
−15=−8a+b
15=−14a+b
15=8a−b
15=−14a+b
30=−6a
a=−5
b=−55
y=−5x−55
3) D=(x,−5x−55)
|SD|2=26
26=(x+14)2+(−5x−55−15)2=x2+28x+196+25x2+700x+4900=26x2+728x+5096
26x2+728x+5096−26=0
26x2+728x+5070=0
x2+28x+195=0
Δ=784−780=4
x1=−15
x2=−13
D1=(−15,20) <− odrzucam
D2=(−13,10)
4) prosta CS:
14=−9a+b
15=−14a+b
−14=9a−b
15=−14a+b

 →
SC=[−5,−1]
R2= |SC|2=26
→
SC=[−5,−1]
R2= |SC|2=26
 dokończ..........
dokończ..........



 Próbowałem coś na początku z podobieństwa, ale, że chodziło o współrzędne punktu, to nie
wiedziałem jak to ugryźć, więc zrobiłem jak umiem
Próbowałem coś na początku z podobieństwa, ale, że chodziło o współrzędne punktu, to nie
wiedziałem jak to ugryźć, więc zrobiłem jak umiem
 Jeżeli ABC leża na jednej prostej i BC=k*AB
to XBC=k* xAB i yBC=k* yAB czy to rozumiesz
Jeżeli ABC leża na jednej prostej i BC=k*AB
to XBC=k* xAB i yBC=k* yAB czy to rozumiesz
 ( tylko nie mogę znaleźć błędu w rachunkach
Twój sposób rozwiązania jest najkrótszy ! Łap ..........
( tylko nie mogę znaleźć błędu w rachunkach
Twój sposób rozwiązania jest najkrótszy ! Łap ..........
