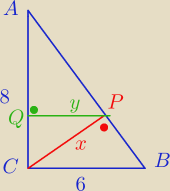
 Mamy
I AB I2 = 82 + 62 = 100
I AB I = 10
PABC = 0,5*8*6 = 24
===================
0,5*10*x = 24 ⇒ 5 x = 24
x = 4,8
IAP I2 = 82 − x2 = 64 − 23,04 = 40,96
I AP I = 6,4
PAPC = 0,5*6,4*4,8 = 15,36
0,5*8*y = 15,36
y = 3,84
I AQI2 = 6,42 − 3,842 = 40,96 − 14,7456 = 26,2144
I AQ I = 5,12
PAPQ = 0,5*5,12*3,84 = 9,8304
==============================
k = 0,4096
Mamy
I AB I2 = 82 + 62 = 100
I AB I = 10
PABC = 0,5*8*6 = 24
===================
0,5*10*x = 24 ⇒ 5 x = 24
x = 4,8
IAP I2 = 82 − x2 = 64 − 23,04 = 40,96
I AP I = 6,4
PAPC = 0,5*6,4*4,8 = 15,36
0,5*8*y = 15,36
y = 3,84
I AQI2 = 6,42 − 3,842 = 40,96 − 14,7456 = 26,2144
I AQ I = 5,12
PAPQ = 0,5*5,12*3,84 = 9,8304
==============================
k = 0,4096
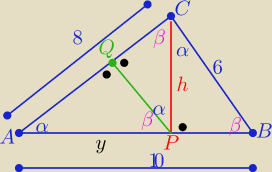 |CP|=h=4,8 P(ABC)= 24
Z podobieństwa trójkątów ABC i APC i APQ z cechy (kkk)
|CP|=h=4,8 P(ABC)= 24
Z podobieństwa trójkątów ABC i APC i APQ z cechy (kkk)
| 8 | y | ||
= | ⇒ y=6,4 | ||
| 10 | 8 |
| P(APQ) | ||
zatem | = k2= (0,64)2= 0,4096 | |
| P(ABC) |