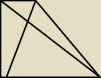
W trapezie równoramiennym ABCD dane sa długości podstaw|AB|=6cm i |CD|=2cm. Marta: W trapezie równoramiennym ABCD dane sa długości podstaw|AB|=6cm i |CD|=2cm oraz ramienia ad = 4 . Oblicz obwód trójkąta AOB gdzie O jest punktem przecięcia przekątnych tego trapezu Pomocy... Strasznie się mecze z tym zadaniem

Marta: Obliczylam że AC=2√5 i BD=2√13 Co dalej?

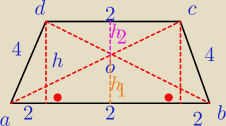f123: h_trapezu = √4² − 2² = √12 = 2√3 Trojkaty AOB i DOC sa podobne −−− cecha kkk

AB
	= 3. Skala podobienstwa −−− 3
DC

h₁ + h₂ = h_trapezu h₁ = 3h₂ 4h₁ = h_trapezu

	√3
h1 =
	2

Dalej sama

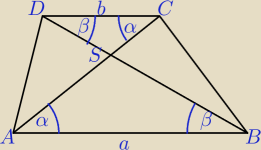Bogdan: Ciekawe zależności w trapezie

	a
Skala podobieństwa trójkątów ABS i CDS k =
	b

Pola trójkątów: P{CDS} = P₁, P_ABS = P₂, P_ASD = P_BSC = P₃ Pole trapezu P_ABCD = P P = ( √P₁ + √P₂ )², P₃ = √ P₁*P₂ P₂ = k²P₁, P₃ = kP₁

	P		k2P		kP
P1 =		, P2 =		, P3 =
	(k + 1)2		(k + 1)2		(k + 1)2

	1
W tym zadaniu h = 2√3, k = 3, P =		*(6 + 2)*2√3 = 8√3,
	2

	32*8√3
P2 =		= ...
	42

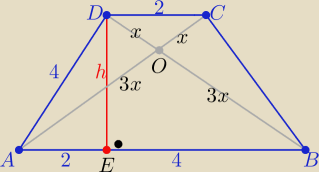Eta: W ΔAED z tw. Pitagorasa : h²=4²−2²= 12 Z podobieństwa trójkątów ABO i DCO z cechy (kkk) w skali k=3 to Obwód ΔABO : L=6x+6 Z tw. Pitagorasa w ΔBED :

	7		√7
(4x)2= h2+42 ⇒ 16x2=12+16⇒ x2=		⇒ x=
	4		2

L=3(√7+2) =========

Marta: Przepraszam ale popełniłam błąd. Tutaj chodi o trapez prostokątny, jak na rysunku

Eta: Jaka treść, taka odpowiedź

Marta: Rozumiem, mój błąd ale wykorzystałam kilka rzeczy i już mam rozwiązanie więc dziekuje

Marta: Właśnie to 3x i 1x wszystko wyjasnilo

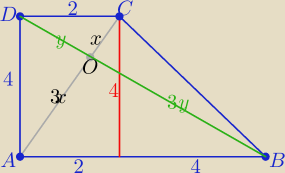Eta: Z tw. Pitagorasa w ΔADC : 16x²=4+16 ⇒ x=........ i z tw. Pitagorasa w ΔABD: 16y²= 16+36 ⇒ y=... Obwód ΔAOB : L= 3(x+y)+6=.... dokończ i po bólu