Metoda Newtona-Raphsona Robert: Stosując metodę Newtona−Raphsona znaleźć rozwiązanie układu równań nieliniowych: a) przybliżone E=|f_i(x₁,x₂)| E<0,3 b) dokładne (f_i(x₁,x₂)=0)

⎧	f1=x12+x22=5
⎩	f2=x12−x22=−3

Chciałem zapytać jak wyznaczyći x⁰, bo bez tego chyba nie da się policzyć ?

ABC: graficznie można startową wartość , na papierze milimetrowym zrób albo na kompie

ABC: tylko jak przyjmiesz za dokładne to nie ma zabawy ... głupi przykład bo widać rozwiązanie x₁=1, x₂=2

Robert: To się poprostu przyjmuje ot tak czy są jakieś obliczenia ?

ABC: teraz biblioteki zamknięte, bym cię odesłał do książki która przystępnie to tłumaczy

ABC: z tego co pamiętam, dawno czytałem, jest tam przykład na metodę której chcesz użyć: https://tezeusz.pl/konorski-b-krysicki-w-nomografia-i-graficzne-metody-obliczeniowe-454139

Robert: Jakim programem można wyznaczyć wartość startową?

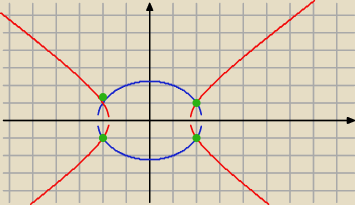
ABC: masz łeb i ch.. to kombinuj ! własną głową kolego wyznaczasz wartość startową , rysując linie o równaniach x² +y² =5 oraz x²−y²=−3 . Jak ładnie narysujesz to otrzymasz przybliżone, a w tym wypadku nawet dokładne rozwiązania

Robert: https://imgur.com/r6I1RkO Tak mi to wyszło. Nadaje się to do czegoś?

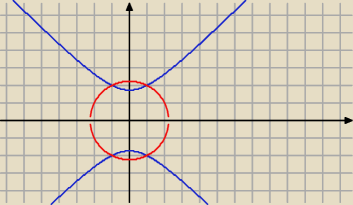
ABC: zapomniałeś o dolnej gałęzi hiperboli, chociaż to polecenie "znaleźć rozwiązanie" to dobry adwokat by wybronił że tylko jedno a nie wszystkie

Robert:

	1 2
Czyli x0=		? Czy to coś jeszcze innego, bo poprzednie przykłady rozwiązywałem licząc

iteracje, aż uzyskałem rozwiązanie przybliżone i dokładne.

Robert:

	1 2
Rozumiem że rozwiązanie dokładne to x0=		, a jak wyznaczyć rozwiązanie przybliżone E<0,3

?

ABC: musisz przyjąć mniej dokładne x₀ mówiłem że to głupie zadanie, wyjdź na przykład od (0.8 1.6)

Robert: A jak uzasadnić że wybrałem wartości 0.8, 1.6 ?

Robert: Ewidentnie punkty przecinają się w 1,2, rzeczywiście głupie zadanie. Dziękuje za pomoc

Robert: A jeszcze chciałbym spytać, można przyjąć 0.9, 1.9? Bo w sumie to mniej liczenia by było

ABC: można, w takich przykładach gdzie nie widać dokładnego rozwiązania staraj się natomiast jak najbliżej przyjmować bo proces może nie być zbieżny

Robert: a graficznie napisać współrzędne te co będę liczył, no nie ?

Robert: W sensie na rysunku zaznaczyć przecięcie dla tych wartości co je będę liczył ?

Robert: czy zaznaczyć dokładne wartości 1,2 ?