Romb milegodnia: W rombie o polu 4,80 dm² poprowadzono odcinek mający 2,4 dm który łączy środki sąsiednich boków rombu przy kącie rozwartym. Oblicz: a) długość przekątnych rombu b) obwód rombu c) wysokość rombu d) pole trójkąta wyciętego z rombu przez dany odcinek

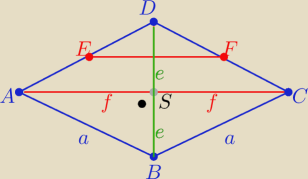
Eta: |EF|=2,4 dm ⇒ 2f=4,8 dm i P=4,8 dm² P=2f*e ⇒ 2e= 1 dm h= √f²+e²= ............ P=a*h ⇒ a= ........ to L=4a=.........

	1		1
P(EFD)=		*		P(rombu)=........
	4		2