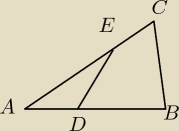
 Na bokach AB i AC trójkąta ABC , który nie jest równoramienny, wybrano takie punkty D i E ,
że |AD | : |DB | = 1 : k oraz |AE | : |EC | = k : 1 , dla k ∈ (0,+ ∞ ) .
Wyznacz wzór funkcji f (k) , która jest zdefiniowana jako stosunek pól trójkątów ADE i ABC .
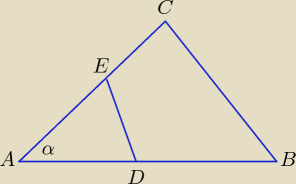
Na bokach AB i AC trójkąta ABC , który nie jest równoramienny, wybrano takie punkty D i E ,
że |AD | : |DB | = 1 : k oraz |AE | : |EC | = k : 1 , dla k ∈ (0,+ ∞ ) .
Wyznacz wzór funkcji f (k) , która jest zdefiniowana jako stosunek pól trójkątów ADE i ABC .
| k*x*y | k | |||
U{PADE}{PABC = | = | |||
| (x(1+k)*y(1+k) | (1+k)2 |

| |AD| | 1 | ||
= | ⇒ |DB| = k*|AD| | ||
| |DB| | k |
| |AE| | |
= k ⇒ |AE| = k*|EC| | |
| |EC| |
| 1 | ||
PADE = | *|AD|*|AE|*sinα | |
| 2 |
| 1 | ||
PABC = | *(|AD| + |DB|)*(|AE| + |EC|)*sinα | |
| 2 |
| PAED | |AD|*|AE| | ||
= | = | ||
| PABC | (|AD| + |DB|)*(|AE| + |EC|) |
| |AD|*k*|EC| | |AD|*k*|EC| | |||
= | = | |||
| (|AD| + k*|AD|)*(k*|EC| + |EC|) | |AD|*|EC|*(k + 1)(k + 1) |
| k | ||
f(k) = | ||
| (k + 1)2 |

